Heuristik eller "ars inveniendi" var namnet på en inte särskilt klart avgränsad speciell forskningsgren, som hörde till logiken eller till filosofin eller till psykologin, ofta beskriven men sällan i detalj och så gott som glömd idag. Heuristikens syfte är att studera metoder och regler för upptäckt och uppfinning. Spår av sådana studier kan man finna i kommentarerna till Euklides. Ett stycke skrivet av Pappus är speciellt intressant i detta avseende. De mest kända försöken att bygga upp ett heuristiskt system gjordes av Descartes och Leibniz, båda stora matematiker och filosofer. Bernard Bolzano gav en anmärkningsvärt detaljerad beskrivning av heuristiken. Föreliggande lilla bok är ett försök att återuppleva heuristiken i en modern och enkel form. Se Modern heuristik.
Adjektivet heuristisk betecknar "som tjänar till att upptäcka eller uppfinna" (på egen hand).
Heuristisk argumentation är en argumentation som inte kan betraktas som strikt och slutgiltig utan bara som möjlig och provisorisk, vars syfte är att leda till upptäckten av det aktuella problemets lösning. Vi måste ofta använda heuristiska argument. Vi når full visshet när vi har kommit till den kompletta lösningen, men innan vi når visshet måste vi ofta nöja oss med en mer eller mindre säker gissning. Vi behöver ofta ett provisorium innan vi kommer till det slutgiltiga. Vi behöver heuristiska resonemang när vi bygger upp ett strikt bevis precis på samma sätt som vi behöver byggnadsställningar när vi bygger ett hus.
Se Tecken på framsteg. Heuristiska argument baseras ofta på induktion eller analogi; se Induktion och matematisk induktion och Analogi, 8, 9, 10.|8|
Heuristiska resonemang är värdefulla i sig själva. Vad som är fel är att förväxla ett heuristiskt argument med ett strängt bevis. Vad som är ännu värre är att utge en heuristisk argumentation för att vara ett strängt bevis.
Undervisningen i vissa ämnen, speciellt integralkalkyl för ingenjörer och fysiker, skulle kunna förbättras väsentligt om man bättre förstod den heuristiska argumentationens art, om man klart insåg både dess fördelar och dess begränsningar, och om läroböckerna framställde sina heuristiska argument på ett öppet sätt. Ett heuristiskt argument som presenteras med omdöme och på ett oförställt sätt kan vara användbart. Det kan bereda vägen för en strängt logisk argumentation, som vanligen redan ingår till en viss del i det heuristiska resonemanget. Men ett heuristiskt resonemang är sannolikt till skada om det förs på ett tvetydigt sätt med en tydlig tvekan mellan skamkänsla och övertygelse. Se Varför behövs bevis?
Hjälpkonstruktioner. Ett problem innehåller mycket mer när vi har slutat arbeta med det än när vi började med det (se Framsteg och prestation, 1). Allteftersom arbetet framskrider lägger vi till nya element till dem vi ursprungligen hade, Ett element som vi inför i hopp om att det skall föra oss fram mot lösningen kallas en hjälpkonstruktion.
1. Det finns olika slag av hjälpkonstruktioner. Om vi löser ett geometriskt problem kan vi föra in nya linjer, hjälplinjer, i vår figur. Om vi löser ett algebraiskt problem kan vi föra in en hjälpstorhet eller hjälpvariabel (se Hjälpproblem, 1). En hjälpsats är en sats vars bevis vi använder i hopp om att det skall föra oss fram mot lösningen till det ursprungliga problemet.
2. Det finns olika skäl för att införa hjälpkonstruktioner. Vi kan vara glada om vi lyckas komma på ett närbesläktat problem som är löst förut. Det är möjligt att vi kan använda ett sådant problem men vi vet ännu inte hur vi skall använda det. Antag t.ex. att det problem vi försöker lösa är ett geometriskt problem och att det närbesläktade problemet som har lösts förut och som vi nu erinrar oss handlar om trianglar. Men det finns ingen triangel i vår figur. För att vi skall kunna använda det gamla problemet måste vi emellertid ha en triangel. Vi måste därför införa en genom att lägga till några lämpliga hjälplinjer i figuren. Har vi erinrat oss ett tidigare löst närbesläktat problem som vi nu önskar använda har vi i allmänhet anledning att ställa frågan: Skulle du kunna införa någon hjälpkonstruktion så att du kan använda det? (Exemplet i avsnitt 10 är typiskt.)
Vi har ett annat tillfälle att införa hjälpelement när vi går tillbaka till definitionerna. Om vi t.ex. skall förklara definitionen av en cirkel bör vi inte enbart nämna medelpunkten och radien utan vi bör också föra in dessa geometriska element i vår figur. Om vi inte gör det skulle vi inte kunna få någon konkret användning av definitionen. Att redogöra för en definition utan att rita samtidigt blir bara tomma ord.
Att försöka utnyttja kända resultat och att gå tillbaka till definitionerna hör till de bästa skälen för att införa hjälpkonstruktioner, men de är inte de enda. Vi kan lägga till hjälpkonstruktioner för att förbättra vår föreställning om problemet, för att göra det fylligare, mer fantasieggande eller för att vi skall komma mera in i det, fastän vi knappast ännu vet hur vi skall kunna utnyttja de element vi lagt till. Vi kanske bara känner att det är en "ljus idé" att föreställa sig problemet på detta sätt med det ena eller andra elementet.
Vi må ha ett eller annat skäl för att införa en hjälpkonstruktion, men vi måste i alla händelser ha något skäl. Vi får aldrig införa en hjälpkonstruktion helt godtyckligt.
3. Exempel. Konstruera en triangel i vilken en vinkel, höjden från denna vinkel och omkretsen är kända.
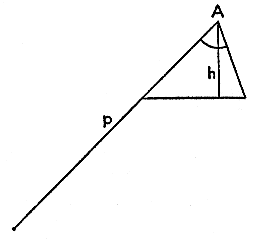 |
Fig. 17 |
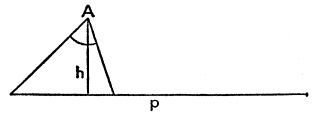 |
Fig. 18 |
Vi inför lämpliga beteckningar. Låt α beteckna den givna vinkeln, h den givna höjden från vinkelns spets A och p den givna omkretsen. Vi ritar en figur i vilken vi lätt placerar in α och h. Har vi använt alla de givna uppgifterna? Nej, vår figur innehåller inte den givna längden p = triangelns omkrets. Därför måste vi införa p. Men hur?
Vi kan försöka föra in p på olika sätt. De försök som visas i fig. 17 och 18 verkar klumpiga. Om vi försöker göra klart för oss varför de förefaller så otillfredsställande kan vi se att det beror på att de inte är symmetriska.
Triangeln har ju tre okända sidor, a, b, c. Vi kallar som vanligt den sida a som står mitt emot A. Nu vet vi att a + b + c = p. Följaktligen spelar sidorna b och c samma roll i problemet. De är utbytbara, problemet är symmetriskt med avseende på b och c. Men b och c spelar inte samma roll i fig. 17 och 18. Genom att vi har ritat in p som vi har gjort har vi behandlat b och c på olika sätt. Fig. 17 och 18 förstör den naturliga symmetrin hos problemet med avseende på b och c. Vi bör därför rita in p så att den har samma relation till b som till c.
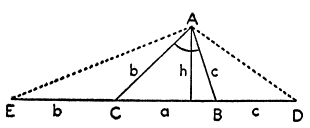 |
Fig. 19 |
Detta resonemang visar sig vara nyttigt genom att det uppmanar oss att placera p som i fig. 19. På ena sidan om triangeln lägger vi ett segment CE av längden b till sidan a och på andra sidan lägger vi ett segment BD av längden c. p framträder därför i fig. 19 som linjen ED med längden b + a + c = p.
Om vi har den minsta erfarenhet av att lösa konstruktionsproblem kan vi inte undvika att jämsides med ED föra in hjälplinjerna AD och AE i figuren. De är vardera bas i en likbent triangel. I själva verket är det mycket lämpligt att i problem införa element som är speciellt enkla och bekanta, såsom likbenta trianglar.
Vi har nu infört våra hjälplinjer på ett mycket lämpligt sätt. Om vi undersöker den nya figuren finner vi att ![]() EAD har ett enkelt samband med den givna vinkeln α. Om vi betraktar de likbenta trianglarna ΔABD och ΔACE finner vi i själva verket att
EAD har ett enkelt samband med den givna vinkeln α. Om vi betraktar de likbenta trianglarna ΔABD och ΔACE finner vi i själva verket att ![]() EAD = α/2 + 90°. Därmed blir det naturligt att i stället försöka konstruera ΔEAD. Men i och med att vi
försöker med denna konstruktion har vi fört in ett hjälpproblem som är betydligt enklare än det ursprungliga problemet.
EAD = α/2 + 90°. Därmed blir det naturligt att i stället försöka konstruera ΔEAD. Men i och med att vi
försöker med denna konstruktion har vi fört in ett hjälpproblem som är betydligt enklare än det ursprungliga problemet.
4. Lärare och läroboksförfattare borde inte glömma att den intelligente eleven och Den intelligente läsaren inte är nöjda med att enbart visa att stegen i en argumentation är riktiga utan att de också vill veta motiven och syftet med de olika stegen. Att införa ett hjälpelement är ett steg som är iögonenfallande. Om en hjälplinje som det vore besvärligt att komma på helt plötsligt uppträder i en figur utan någon som helst motivering och löser problemet på ett överraskande sätt, känner sig intelligenta elever och läsare besvikna. De tycker att de har blivit lurade. Matematik är intressant såtillvida att den tar vår slutledningsförmåga och vår uppfinningsförmåga i anspråk. Men det finns ingenting att lära av en argumentering eller en briljant lösning om motivet och syftet med det mest iögonenfallande steget förblir obegripligt. Att göra sådana steg begripliga genom lämpliga anmärkningar (som under avsnitt 3 ovan) eller genom omsorgsfullt valda frågor och uppmaningar (som i avsnitten 10, 18, 19, 20) tar åtskillig tid och är arbetsamt. Men det kan vara värt mödan.
Hjälpproblem är problem som vi inte använder för deras egen skull utan därför att vi hoppas att med hjälp av dem kunna lösa ett annat problem, det ursprungliga problem vi ställts inför. Det ursprungliga problemets lösning är det mål vi vill nå. Hjälpproblemet är ett medel med vars hjälp vi försöker uppnå målet.
En insekt försöker flyga ut genom en fönsterruta, försöker samma sak om och om igen men prövar inte nästa fönster som står öppet och genom vilket den kom in i rummet. En människa kan eller borde kunna handla på ett mer intelligent sätt. Mänsklig överlägsenhet består i att gå runt ett hinder som inte kan övervinnas direkt, att hitta på något lämpligt hjälpproblem när det ursprungliga problemet ter sig olösligt. Att tänka ut ett hjälpproblem är en viktig tankeoperation. Att ställa upp ett nytt klart problem som är underordnat ett annat problem, att klart inse att dess syfte är betydelsefullt för ett annat syfte, är en förfinad intelligensprestation. Det är en viktig uppgift att lära (eller lära ut) hur man skall handskas på ett intelligent sätt med hjälpproblem.
1. Exempel. Lös ekvationen x4 - 13x² + 36 = 0.
Om vi lägger märke till att x4 = (x²)² inser vi nog fördelen med att införa y = x². Vi har nu ett nytt problem: Lös ekvationen y² - 13y + 36 = 0.
Det nya problemet är ett hjälpproblem. Vi tänker använda det som ett medel att lösa vårt ursprungliga problem. Den okända storheten i vårt hjälpproblem, y, kan lämpligen betecknas som hjälpvariabel.
2. Exempel. Sök diagonalen i en rektangulär parallellepiped om längden av tre sidor, som alla utgår från samma hörn, är givna.
När vi försöker lösa detta problem (avsnitt 8) kanske vi genom analogi (avsnitt 15) kommer till ett annat problem: Sök diagonalen i en rektangulär parallellogram om längden av två sidor dragna från samma hörn är givna.
Det nya problemet är ett hjälpproblem. Vi studerar det eftersom vi hoppas kunna få någon hjälp av det när vi löser vårt ursprungliga problem.
3. Fördelar. Den nytta vi kan ha av att föra in ett hjälpproblem kan vara av olika slag. Vi kan kanske använda hjälpproblemets resultat. Om vi sålunda i exempel 1 har funnit att y = 4 eller 9 genom att lösa andragradsekvationen för y, får vi att x² = 4 eller att x² = 9 och kan således härleda de möjliga värdena på x.
I andra fall kanske vi kan använda hjälpproblemets metod. I exempel 2 är hjälpproblemet ett plangeometriskt problem. Det är analogt med men enklare än det ursprungliga problemet, som är ett rymdgeometriskt problem. Det är lämpligt att införa ett hjälpproblem av detta slag i förhoppningen att det skall kunna ge utbyte, att det skall kunna ge oss tillfälle att lära känna vissa metoder, operationer eller hjälpmedel, som vi sedan kan använda i det ursprungliga problemet. Hjälpproblemet i exempel 2 är lyckligt valt. Om vi undersöker det närmare finner vi att vi kan använda både dess metod och dess resultat. (Se avsnitt 15 och Använde du alla de givna uppgifterna?)
4. Risker. Den tid och det arbete vi lägger ner på hjälpproblemet drabbar ju det ursprungliga problemet. Om undersökningen av hjälpproblemet inte ger resultat kan tid och arbete alltså vara bortkastade. Därför måste vi använda vårt omdöme när det gäller att välja hjälpproblem. Vi kan ha flera goda skäl för vårt val. Hjälpproblemet kanske verkar mer tillgängligt än det ursprungliga problemet. Det kanske verkar mer lärorikt eller det kanske har något slags estetisk attraktion. Ibland är den enda fördelen med hjälpproblemet att det är nytt och erbjuder oanade möjligheter. Vi väljer det eftersom vi är trötta på det ursprungliga problemet vars angreppspunkter tycks vara uttömda.
5. Hur man finner ett hjälpproblem. Att man upptäcker lösningen till ett givet problem är ofta en följd av att man finner ett lämpligt hjälpproblem. Olyckligtvis finns det ingen osviklig metod för att komma på lämpliga hjälpproblem, precis som det inte finns någon osviklig metod för att finna lösningen. Det finns emellertid frågor och uppmaningar som ofta kan vara till god hjälp, såsom Betrakta den obekanta. Vi kommer ofta fram till ett användbart hjälpproblem genom att Variera problemet.
6. Ekvivalenta problem. Två problem är ekvivalenta om lösningen till det ena innebär lösningen till det andra. I vårt exempel 1 är det ursprungliga problemet och hjälpproblemet ekvivalenta.
Betrakta följande satser.
Dessa två satser är inte identiska. De innehåller olika begrepp eftersom den ena handlar om likheten mellan sidor och den andra om likheten mellan vinklar i en triangel. Men var och en av satserna följer av den andra. Problemet att bevisa A är därför ekvivalent med problemet att bevisa B.
Om vi vill bevisa A kan det vara fördelaktigt att införa problemet att bevisa B som ett hjälpproblem. Sats B är något lättare att bevisa än A och, vad som är viktigare, vi kan förutse att B är lättare än A. Förmodligen bedömer vi det så, det tycks redan från början troligt att B är lättare än A. Eftersom sats B enbart handlar om vinklar är det mer "homogent" än sats A som handlar om både vinklar och sidor.
Övergången från det ursprungliga problemet till hjälpproblemet kallas omvändbar reduktion, konvertibel, bilateral eller ekvivalent reduktion om de två problemen är ekvivalenta. Så är t.ex. reduktionen från A till B (se ovan) omvändbar och samma sak gäller för reduktionen i exempel 1. Omvändbar reduktion är i vissa avseenden viktigare och lämpligare än andra sätt att införa hjälpproblem, men hjälpproblem som inte är ekvivalenta med det ursprungliga problemet kan också vara mycket användbara, se exempel 2.
7. Kedjor av ekvivalenta hjälpproblem är vanliga i matematiska resonemang. Antag att vi skulle vilja lösa problem A, men vi kan inte se lösningen. Så finner vi att A är ekvivalent med ett annat problem B. Betraktar vi B kommer vi kanske in på ett tredje problem C ekvivalent med B. Fortsätter vi på samma sätt reducerar vi problem C till D osv. tills vi kommer till ett sista problem L vars lösning är känd eller uppenbar. Eftersom varje problem är ekvivalent med det föregående måste det sista problemet L vara ekvivalent med vårt ursprungliga problem A. Följaktligen kan vi sluta oss till lösningen på det ursprungliga problemet A ur problem L, vilket vi träffade på som sista länken i en kedja av hjälpproblem.
Problemkedjor av detta slag uppmärksammades av grekiska matematiker, vilket framgår av ett viktigt avsnitt hos Pappus.
Som en illustration kan vi studera vårt exempel 1. Låt (A) beteckna det villkor som ställs på den okända storheten x:
(A)x4 - 13x² + 36 = 0
Ett sätt att lösa detta problem är att transformera detta villkor till ett annat villkor som vi kallar (B):
(B)(2x²)² - 2(2x²)13 + 144 = 0
Observera att villkoren (A) och (B) är olika. De är endast obetydligt olika om man så vill och de är med säkerhet ekvivalenta som man lätt kan övertyga sig om, men de är absolut inte identiska. Övergången från (A) till (B) är inte bara korrekt utan har också ett klart syfte, uppenbart för var och en som känner till hur man löser en andragradsekvation. Går vi vidare i samma riktning transformerar vi villkoret (B) till ännu ett annat villkor (C):
(C)(2x²)² - 2(2x²)13 + 169 = 25
Fortsätter vi på samma sätt får vi
(D)(2x²-13)² = 25
(E)2x² - 13 = ±5
(F)![]()
(G)![]()
(H)x = 3, -3, 2 eller -2
Varje reduktion vi har gjort har varit omvändbar. Följaktligen är det sista villkoret (H) ekvivalent med det första villkoret (A) så att alltså 3, -3, 2, -2 alla är möjliga lösningar till vår ursprungliga ekvation.
I det föregående härledde vi ur det ursprungliga vilkoret (A) en följd av villkor (B), (C), (D), …, vart och ett ekvivalent med det föregående. Denna procedur kräver den största noggrannhet. Villkor som är ekvivalenta uppfylls av samma objekt. Om vi därför går över från ett givet villkor till ett nytt villkor som är ekvivalent med det förra, har vi också samma lösningar. Men om vi går över från ett givet villkor till ett som är snävare, mer inskränkt, förlorar vi lösningar. Går vi över till ett villkor som är vidare tillåter vi oegentliga, tillfälliga lösningar, som inte har någonting att göra med det givna problemet. Om vi i en serie av successiva reduktioner går över till ett snävare och sedan till ett vidare villkor kan vi tappa bort det ursprungliga problemet fullständigt. För att undvika denna risk måste vi noga kontrollera varje nytt infört villkor. Är det ekvivalent med det ursprungliga villkoret? Denna fråga är ännu viktigare när vi inte handskas med bara en ekvation som här utan med ett ekvationssystem, eller när villkoret inte uttrycks med hjälp av ekvationer som t.ex. när det gäller geometriska konstruktionsproblem.
(Jämför Pappus, speciellt avsnitt 2, 3, 4, 8. Beskrivningen där är onödigt begränsad. Den beskriver en kedja av "sökproblem", som alla har olika okända storheter. Det exempel vi studerade ovan har precis motsatt egenskap: Alla problem i kedjan har samma obekanta storhet och skiljer sig enbart i villkorets form. Naturligtvis är en sådan begränsning inte nödvändig.)
8. Ensidig reduktion. Vi har två olösta problem, A och B. Om vi kunde lösa A skulle vi härav kunna härleda den fullständiga lösningen till B, men inte omvänt. Om vi kunde lösa B skulle vi möjligen kunna få någon information om A, men vi skulle inte veta hur vi kommer fram till den fullständiga lösningen till A genom att vi vet lösningen till B. I ett sådant fall uppnår vi mer genom att lösa A än genom att lösa B. Låt oss kalla A det mer ambitiösa och B det mindre ambitiösa av de två problemen.
Om vi från ett visst problem går över till ett mer ambitiöst eller till ett mindre ambitiöst problem kallar vi detta steg för ensidig reduktion. Det finns två slag av ensidig reduktion, och båda är på ett eller annat sätt vanskligare än en omvändbar (bilateral, tvåsidig) reduktion.
Exempel 2 visar en ensidig reduktion till ett mindre ambitiöst problem. Om vi kunde lösa det ursprungliga problemet, som handlar om en parallellepiped vars längd, bredd och höjd är resp. a, b, c, så skulle vi i själva verket kunna gå vidare till hjälpproblemet genom att sätta c = 0 och få en parallellogram med längden a och bredden b. Ett annat exempel på ensidig reduktion till ett mindre ambitiöst problem tas upp i Specialisering, 3, 4, 5. Dessa exempel visar att vi med litet tur mycket väl kan använda ett mindre ambitiöst hjälpproblem som en språngbräda, om vi kombinerar hjälpproblemets lösning med någon lämplig ytterligare iakttagelse för att komma fram till det ursprungliga problemets lösning. Ensidig reduktion till ett mer ambitiöst problem kan också ge resultat. (Se Generalisering, 2, samt reduktionen av det första till det andra problemet i Induktion och matematisk induktion, 1, 2.) I själva verket kan det mer ambitiösa problemet vara mer lättillgängligt. Detta är innebörden av Uppfinnarparadoxen.
Här är ett närbesläktat problem som är löst förut. Detta är goda nyheter. Ett problem som har samband med det föreliggande problemet och vars lösning är känd är verkligen välkommet. Det är ännu mer välkommet om sambandet är nära och lösningen enkel. Chanserna är stora att ett sådant problem kommer att vara användbart när man löser det aktuella problemet.
Den situation vi diskuterar här är typisk och viktig. För att klart inse detta kan vi jämföra med den situation vi befinner oss i när vi arbetar på ett hjälpproblem. I båda fallen vill vi lösa ett visst problem A och vi inför och studerar ett annat problem B i hopp om att vi kan ha någon nytta av det för att lösa det givna problemet A. Skillnaden ligger i vår relation till B. I det ena fallet lyckades vi komma på ett gammalt problem B vars lösning vi känner utan att ännu veta hur vi skall använda den. I det andra fallet lyckades vi konstruera ett nytt problem B. Vi vet (eller åtminstone misstänker vi starkt) hur vi skall använda problemet B, men vi vet ännu inte hur vi skall lösa det. Denna svårighet med B utgör skillnaden mellan de två fallen. När vi har övervunnit den kan vi använda B på samma sätt i båda fallen. Vi kan använda resultatet eller metoden (som visats i Hjälpproblem, 3) och om vi har tur kanske både resultatet och metoden. I den situation vi befinner oss nu känner vi lösningen på B men vi vet ännu inte hur vi skall använda den. Därför frågar vi: Skulle du kunna använda det? Skulle du kunna använda dess resultat? Eller dess metod?
Avsikten att använda ett visst tidigare löst problem påverkar vår föreställning om det föreliggande problemet. När vi försöker koppla samman de två problemen, det nya och det gamla, för vi in element i det nya problemet som motsvarar vissa element i det andra problemet. Vårt problem är t.ex. att bestämma den omskrivna sfären till en given tetraeder. Det är ett rymdgeometriskt problem. Vi kanske erinrar oss att vi förut har löst det analoga problemet i plan geometri: att konstruera den omskrivna cirkeln till en given triangel. Då påminner vi oss att vi i det gamla plangeometriska problemet använde transversaler dragna från mitten av varje sida i triangeln. (Transversalerna skär varandra i cirkelns medelpunkt.) Det är rimligt att försöka införa någonting analogt i det aktuella problemet. Alltså inför vi nu motsvarande hjälpelement, nämligen plan som skär vinkelrätt genom mittpunkten av varje kant till tetraedern. Efter denna idé kommer vi lätt fram till lösningen av vårt rymdgeometriska problem genom att bara följa den analoga lösningen i plan geometri.
Föregående exempel är typiskt. Genom att betrakta ett förut löst, närbesläktat problem kommer vi på vilka hjälpkonstruktioner vi behöver. Införandet av dessa hjälpkonstruktioner gör det möjligt för oss att använda det närbesläktade problemet i full utsträckning när vi löser vårt aktuella problem. Detta är vad vi strävar efter när vi för att få reda på om ett tidigare löst närbesläktat problem kan användas ställer frågan: Skulle man kunna införa någon hjälpstorhet så att man kan använda det?
Här är en närbesläktad sats som är bevisad förut. Detta är en variant av vad som diskuterats här och den exemplifieras i avsnitt 19.
Induktion och matematisk induktion. Induktion är en process för att upptäcka allmänna lagar genom att iaktta och kombinera speciella fall. Den används i alla vetenskaper, även inom matematik. Matematisk induktion används enbart inom matematiken och då för att bevisa satser av ett visst slag. Det är olyckligt att uttrycken är besläktade eftersom det finns mycket litet logiskt samband mellan de två processerna. Det finns emellertid ett praktiskt samband. Vi använder ofta båda metoderna tillsammans. Vi illustrerar nu båda metoderna med hjälp av samma exempel.
1. Vi kanske av en ren tillfällighet observerar att 1 + 8 + 27 + 64 = 100, och när vi upptäckt kuberna och kvadraten kan vi skriva detta faktum i den intressantare formen 1³ + 2³ + 3³ + 4³ = 10². Hur inträffar något sådant? Inträffar det ofta att en summa av successiva kuber är en kvadrat?
När vi frågar detta liknar vi vetenskapsmannen som, efter det att en egendomlig växt eller en egendomlig geologisk formation har gjort ett starkt intryck på honom, formulerar en allmän frågeställning. Vår allmänna fråga handlar om summan av successiva kuber, 1³ + 2³ + 3³+ … + n³. Vi leddes till denna genom det "speciella fallet" n = 4.
Vad gör vi för att besvara frågan? Samma sak som vetenskapsmannen skulle göra. Vi undersöker andra speciella fall. Specialfallen n = 2, 3 är ännu enklare, fallet n = 5 kommer härnäst. Låt oss även ta med fallet n = 1 för konsekvensens och fullständighetens skull. Om vi ordnar dessa fall snyggt och prydligt som en geolog skulle ordna sina malmprover, erhåller vi följande tabell:
| 1 | = | 1 | = | 1² |
| 1 + 8 | = | 9 | = | 3² |
| 1 + 8 + 27 | = | 36 | = | 6² |
| 1 + 8 + 27 + 64 | = | 100 | = | 10² |
| 1 + 8 + 27 + 64 + 125 | = | 225 | = | 15² |
Det är svårt att tro att alla dessa summor av på varandra följande kuber är kvadrater av ren tillfällighet. I liknande fall skulle naturvetaren knappast tvivla på att den allmänna lag som antyds av specialfallen han observerat är korrekt. Den allmänna lagen är nästan bevisad genom induktion. Matematikern uttrycker sig något försiktigare fastän han naturligtvis i grund och botten tänker på samma sätt. Han skulle säga att följande sats mycket starkt antyds genom induktion:
Summan av de första n kuberna är en kvadrat.
2. Vi har letts till att gissa en märklig, något mystisk lag. Varför skulle summan av på varandra följande kuber vara en kvadrat? Men uppenbarligen är den en kvadrat.
Vad skulle naturvetaren göra i en sådan situation? Han skulle gå vidare med att pröva sin gissning. Han kan då utföra undersökningen på olika sätt. Kanske samlar han ytterligare experimentellt bevismaterial. Om vi vill göra samma sak måste vi undersöka de fall som kommer härnäst, n = 6, 7, … Naturvetaren kanske också ånyo undersöker de fakta som ledde honom till gissningen. Han jämför dem noggrant, han försöker att plocka fram någon djupare regelbundenhet, någon ytterligare analogi. Låt oss följa denna metod.
Vi undersöker alltså åter fallen n = 1, 2, 3, 4, 5 vilka vi har ordnat i vår tabell. Varför är alla dessa summor kvadrater? Vad kan vi säga om dessa kvadrater? Deras baser är 1, 3, 6, 10, 15. Vad är detta för tal? Finns det någon djupare regelbundenhet, någon ytterligare analogi? I vilket fall som helst tycks de inte öka alltför oregelbundet. Hur ökar de? Skillnaden mellan på varandra följande termer i denna följd är själv ökande, 3 - 1 = 2, 6 - 3 = 3, 10 - 6 = 4, 15 - 10 = 5.
Dessa skillnader är emellertid regelbundna på ett iögonenfallande sätt. Vi kan här se en förvånande analogi mellan kvadraternas baser, en anmärkningsvärd regelbundenhet i talen 1, 3, 6, 10, 15:
| 1 | = | 1 |
| 3 | = | 1 + 2 |
| 6 | = | 1 + 2 + 3 |
| 10 | = | 1 + 2 + 3 + 4 |
| 15 | = | 1 + 2 + 3 + 4 + 5 |
Om denna regelbundenhet är allmän (motsatsen är svår att tro) antar vår förmodade sats en mer precis form nämligen 1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)² för n = 1, 2, 3, …
3. Den lag vi just formulerat fann vi genom induktion och det sätt vi fann den på ger oss en föreställning om induktion som nödvändigtvis är ensidig och ofullständig men inte förvrängd. Induktion försöker att finna regelbundenhet och sammanhang bakom iakttagelserna. Dess mest framstående hjälpmedel är generalisering, specialisering, analogi. En preliminär generalisering formuleras ur försöken att förstå iakttagna fakta. Den baseras på analogi och testas genom ytterligare specialfall.
Vi avstår från ytterligare kommentarer om induktion, om vilken det råder mycket delade meningar bland filosofer. Men det kan tilläggas att många matematiska resultat först har härletts genom induktion och bevisats senare. Matematik sådan den ter sig i en strängt logisk framställning är en systematisk, deduktiv vetenskap, men matematik sådan den är när den håller på att utforskas är en experimentell, induktiv vetenskap.
4. I matematik som i fysik kan vi använda iakttagelse och induktion för att upptäcka allmänna lagar. Men det finns en skillnad. I fysiken finns det ingen högre auktoritet än iakttagelse och induktion medan det i matematiken finns en sådan auktoritet: strängt logiskt bevis.|9|
Sedan vi har arbetat experimentellt någon tid kan det vara bra att ändra vår syn på frågan. Låt oss vara strängt logiska. Vi har upptäckt ett intressant resultat men resonemanget som ledde till det var endast sannolikt, experimentellt, provisoriskt, heuristiskt. Låt oss försöka fastställa det definitivt genom ett strängt logiskt bevis.
Vi har nu kommit till ett "bevisproblem": Att bevisa eller att vederlägga det förut formulerade resultatet (se 2 ovan).
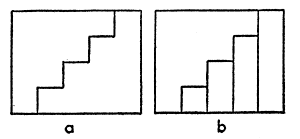 |
Fig. 20. |
En liten förenkling kan göras. Kanske vet vi att 1 + 2 + 3 + … + n = n(n + 1)/2. Hur som helst är detta lätt att bevisa. Gör en rektangel med sidorna n och n + 1 och dela in den i två halvor med sicksacklinjen enligt fig. 20 a, som visar fallet n = 4. Vardera halvan är "trappformad" och för ytan gäller uttrycket 1 + 2 + … + n, för n = 4 är den alltså 1 + 2 + 3 + 4, se fig. 20 b. Hela rektangelns yta är nu n·(n + 1), och eftersom den trappformade ytan utgör hälften är sambandet ovan visat.
Vi skriver nu om resultatet vi funnit genom induktion till
![]()
5. Om vi inte har någon som helst ide om hur vi skall bevisa detta samband kan vi åtminstone pröva det. Låt oss ta det första fall vi ännu inte har prövat nämligen n = 6. För detta fall ger formeln
![]()
vilket visar sig stämma ty om vi räknar ut båda leden blir de vardera lika med 441.
Vi kan pröva formeln på ett mer effektivt sätt. Formeln är med mycket stor sannolikhet allmänt giltig för alla värden på n. Förblir den giltig när vi går över från något värde n till nästa värde n+ 1? I likhet med sista formeln i förra avsnittet skall alltså gälla
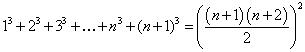
Nu kan vi göra en enkel kontroll, Subtraherar vi ekvationen från avsnitt 4 från ovanstående ekvation erhåller vi
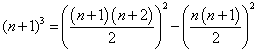
Denna ekvation är emellertid lätt att pröva. Högra sidan kan skrivas om
![]()
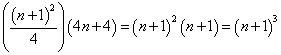
Vår experimentellt funna formel har sålunda bestått ett viktigt prov.
Låt oss se exakt vad testet innebär. Vi har bevisat att
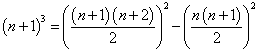
Vi vet inte än huruvida
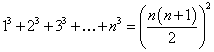
är sant. Men om vi visste att det var sant skulle vi genom att addera den ekvation vi nyss bevisat kunna dra slutsatsen att
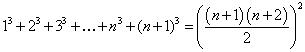
också är sann, vilket innebär att satsen även gäller för nästa heltal n + l. Nu vet vi faktiskt att vår förmodan är riktig för n = 1, 2, 3, 4, 5, 6. Men om den är riktig för n = 6 måste den även, i kraft av vad vi nyss visat, vara riktig för n = 7. Är vår förmodan riktig för n = 7 är den också sann för n = 8, är den riktig för n = 8 är den emellertid också riktig även för n = 9 osv. Den gäller för alla n, den har visats ha allmän giltighet.
6. Föregående bevis kan tjäna som mönster för många liknande fall. Vilka är de väsentliga dragen i detta mönster?
Det påstående vi vill bevisa måste vara givet i förväg och i preciserad form.
Påståendet måste innehålla ett beroende av ett heltal n.
Påståendet måste vara tillräckligt explicit så att vi har möjlighet att pröva om det förblir sant när vi går över från n till nästa heltal n + 1.
Om testet utfaller positivt i ett konkret fall kan vi kanske använda den erfarenhet vi vann under testet för att bevisa att påståendet måste vara sant för n + 1 såvida det är sant för n. När vi har kommit så långt är det tillräckligt att veta att påståendet är sant för n = 1. Därav följer att det gäller för n = 2 och sedan för n = 3 osv. Genom att gå över från ett heltal till nästa visar vi att påståendet gäller allmänt.
Denna process används så ofta att den förtjänar en beteckning. Vi skulle kunna kalla den "bevis från n till n + 1" eller ännu enklare "övergång till nästa heltal". Olyckligtvis har "matematisk induktion" accepterats som fackterm. Denna term beror på en tillfällighet. Det preciserade påstående vi har att bevisa kan ha kommit ur vilken källa som helst och det är ur logisk synpunkt oväsentligt hur vi funnit det. I många fall, liksom i det fall vi diskuterat i detalj ovan, är källan induktion. Vi har funnit sambandet experimentellt och därför kan beviset förefalla som ett matematiskt komplement till induktion och härav namnet.
7. Det finns en annan punkt som är något subtil men viktig för var och en som själv vill konstruera bevis. I det föregående fann vi två olika samband genom iakttagelse och induktion, det ena efter det andra, det första i avsnitt 1, det andra i avsnitt 2. Det andra var mer preciserat än det första.
När vi sysslade med det andra sambandet fann vi en möjlighet att kontrollera övergången från n till n + 1, och på så vis lyckades vi finna ett bevis genom "matematisk induktion". Genom att bara betrakta det första sambandet utan att lägga till den precision som är innefattad i det andra skulle vi knappast ha kunnat komma på ett sådant bevis. I själva verket är det första påståendet mindre precist, mindre "explicit", mindre "påtagligt", mindre tillgängligt för prövning och kontroll än det andra. övergången från det första till det andra, från det mindre till det mer preciserade påståendet, utgjorde en viktig förberedelse till det slutliga beviset.
Denna omständighet har en paradoxal aspekt. Det andra påståendet är starkare. Det inbegriper omedelbart det första, medan det något diffusa första påståendet knappast kan inbegripa det mer pregnanta andra påståendet. Alltså är den starkare satsen lättare att bemästra än den svagare. Detta är Uppfinnarparadoxen.
Kan du använda resultatet? Att själv finna lösningen till ett problem är att göra en upptäckt. Om problemet inte är svårt är upptäckten kanske inte så betydelsefull, men det är icke desto mindre en upptäckt. Har vi gjort en om än aldrig så blygsam upptäckt borde vi alltid fråga oss om det möjligen ligger någonting mera bakom den. Vi borde ta vara på de möjligheter som det nya resultatet öppnar. Vi borde försöka att igen använda den metod som vi har använt. Utnyttja din framgång! Kan du använda resultatet eller metoden för något annat problem?
1. Vi kan lätt föreställa oss nya problem om vi är något så när förtrogna med de viktigaste sätten att variera ett problem, såsom Generalisering, Specialisering, Analogi och Uppdelning och rekombinering. Vi börjar från ett givet problem och härleder ur detta andra problem med hjälp av de nämnda metoderna, och från de problem vi då erhåller härleder vi ytterligare andra osv. Proceduren är teoretiskt obegränsad, men i praktiken går vi inte särskilt långt, eftersom de nya problem vi erhåller lätt blir otillgängliga.
Å andra sidan kan vi konstruera nya problem som lätt kan lösas genom att använda lösningen till ett tidigare löst problem. Men dessa lätta nya problem blir gärna ointressanta.
Att finna nya problem som är både intressanta och tillgängliga är inte så lätt. Vi behöver erfarenhet, omdöme och en smula tur. Ändå bör vi inte försumma att se oss omkring efter flera goda problem när vi har lyckats lösa ett. Goda problem och champinjoner har någonting gemensamt. De växer i klungor. Har man gjort ett fynd bör man titta sig omkring. Det är troligt att det finns flera i närheten.
2. Vi skall illustrera några av punkterna ovan med hjälp av samma exempel som vi diskuterade i avsnitten 8, 10, 12, 14, 15. Vi utgår alltså från följande problem:
Sök diagonalen i en rektangulär parallellepiped vars tre dimensioner (längd, bredd och höjd) är givna.
Om vi känner lösningen till detta problem kan vi lätt lösa vilket som helst av följande problem (av vilka de första två antyddes i avsnitt 14).
Sök radien av den omskrivna sfären till en given rektangulär parallellepiped.
Höjden i en rektangulär pyramid har basrektangelns medelpunkt som fotpunkt. Beräkna längden av sidokanterna om pyramidens höjd och sidorna i dess bas är givna.
Sök avståndet mellan två punkter vars rektangulära koordinater (x1, yl, z,), (x2, y2, z2) är givna.
Vi löser dessa problem med lätthet eftersom de knappast skiljer sig från det ursprungliga problem som vi känner lösningen till. I de olika fallen har vi lagt till något nytt begrepp till vårt ursprungliga problem, såsom omskriven sfär, pyramid, rektangulära koordinater. Det går lätt att lägga till dessa begrepp och det är lätt att eliminera dem, och när vi har blivit av med dem kommer vi tillbaka till det ursprungliga problemet.
Problemen ovan har ett särskilt intresse eftersom de införda begreppen är intressanta. Det sista problemet, det om avståndet mellan två punkter uttryckta med hjälp av deras koordinater, är t.o.m. ett viktigt problem eftersom rektangulära koordinater är viktiga.
3. Här är ytterligare ett problem som vi lätt kan lösa om vi vet lösningen till det ursprungliga problemet: Sök höjden i en rektangulär parallellepiped om längden, bredden och en diagonal är givna.
Lösningen till vårt ursprungliga problem består i själva verket väsentligen i att ställa upp ett samband mellan fyra storheter, de tre kantlängderna i parallellepipeden och dess diagonal. Om tre vilka som helst av dessa fyra storheter är givna kan vi beräkna den fjärde ur sambandet. Vi kan alltså lösa det nya problemet.
Här har vi ett mönster för att härleda nya lättlösta problem ur ett tidigare löst problem. Vi betraktar den ursprungliga obekanta storheten som given och någon av de ursprungliga givna storheterna som okänd. Sambandet mellan de okända och de givna storheterna är samma i båda problemen, både det gamla och det nya. Har vi funnit detta samband i det ena problemet kan vi använda det i det andra.
Detta sätt att härleda nya problem genom att "byta roller" skiljer sig mycket från det mönster vi använde i avsnitt 2.
4. Låt oss nu härleda några nya problem med andra metoder.
En naturlig generalisering av vårt ursprungliga problem är följande: Beräkna diagonalen i en parallellepiped om man känner de tre kanter som utgår från diagonalens ena ändpunkt samt de tre vinklarna mellan dessa tre kanter.
Genom specialisering erhåller vi följande problem: Beräkna diagonalen i en kub med given kantlängd.
Vi kan komma fram till en outtömlig mängd av problem med hjälp av analogi. Här är ett par som härletts ur problemen i avsnitt 2. Sök diagonalen i en reguljär oktaeder med given kantlängd. Sök radien i den omskrivna sfären till en reguljär tetraeder med given kantlängd. Beräkna avståndet mellan två punkter på jordytan (det sfäriska avståndet) om punkternas geografiska koordinater, latitud och longitud, är givna. (Jordens yta betraktas som sfärisk.)
Dessa problem är alla intressanta men endast det som vi fått genom specialisering kan lösas omedelbart på grundval av lösningen till vårt ursprungliga problem.
5. Vi kan härleda nya problem ur ett tidigare genom att betrakta några av dess element som variabla.
Ett specialfall av ett problem omnämnt i avsnitt 2 är problemet att finna radien i en sfär omskriven kring en kub vars kant är given. Låt oss betrakta kuben och den gemensamma medelpunkten för kub och sfär som bestämda men låt oss variera sfärens radie. Om radien är liten ligger sfären inuti kuben. Allteftersom radien ökar expanderar sfären (som en gummiballong som håller på att blåsas upp). I ett visst ögonblick tangerar sfären kubens ytor, litet senare dess kanter och därefter passerar sfären genom hörnen. Vilka värden antar radien vid dessa tre kritiska ögonblick?
6. Den matematiska erfarenheten hos en elev är ofullständig om han aldrig har fått tillfälle att lösa ett problem som han eller hon uppfunnit själv. Läraren kan visa hur man härleder nya problem ur ett som just har lösts och därigenom väcka elevernas nyfikenhet. Läraren kan också lämna en del av upptäckten till eleverna. Han kan t.ex. berätta om den expanderande sfär vi just diskuterat ovan (avsnitt 5) och fråga: "Vad skulle du försöka att beräkna? Vilket värde på radien är speciellt intressant?"
Kan du härleda resultatet på något annat sätt? När den lösning som vi slutligen har kommit fram till är lång och invecklad är det naturligt att misstänka att det finns någon lösning som är klarare och mera direkt: Kan du härleda resultatet på något annat sätt? Kan du se det direkt? Även om vi har lyckats finna en tillfredsställande lösning kan vi kanske ändå vara intresserade av att finna en annan lösning. Vi vill övertyga oss om giltigheten av vårt teoretiska resultat genom två skilda härledningar precis som vi kan vilja förnimma ett föremål med hjälp av två olika sinnen. Efter att ha funnit ett bevis vill vi kanske se ett annat bevis, precis som vi vill vidröra ett föremål sedan vi har sett det.
Två bevis är bättre än ett. Man ligger säkrare förtöjd om man har kastat ut två ankare.
1. Exempel. Beräkna storleken S av mantelytan hos en stympad rät cirkulär kon om höjden är h och de övre och undre sidornas radier är r resp. R.
Detta problem kan lösas med olika metoder. Kanske kan vi t.ex. formeln för mantelytan hos en kon. Eftersom vi får den stympade konen genom att av en viss kon skära av en mindre kon, så kan vi få mantelytan som skillnaden mellan två hela koniska ytor. Det återstår bara att uttrycka dem i R, r och h. Om vi genomför denna plan erhåller vi slutligen formeln S = π(R + r) √[(R - r)² + h²]. När vi har funnit denna lösning på ett eller annat sätt efter en längre beräkning kanske vi vill ha ett klarare och mera direkt svar. Kan du härleda resultatet på något annat sätt? Kan du se det direkt?
| Fig. 21 | 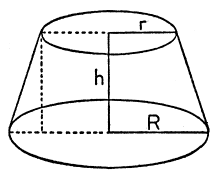 |
Om vi vill försöka se hela resultatet intuitivt kan vi börja med att försöka inse den geometriska betydelsen av de olika delarna. Då lägger vi märke till att √[(R - r)² + h²] är längden av den sluttande höjden. (Den sluttande höjden är en av de icke-parallella sidorna i det likbenta parallelltrapets som genererar den stympade konen när det roterar omkring sin symmetriaxel, se fig. 21.) Sedan kanske vi upptäcker att π(R + r) = (2πR + 2πr)/2 är medelvärdet av omkretsens värde vid den övre och undre ytan. Tittar vi på formeln kan vi finna det motiverat att skriva om den som π(R + r) = 2π(R + r)/2, dvs. som omkretsen på mitten av den stympade konen ( = omkretsen av det tvärsnitt som ligger mitt emellan den övre och den undre ytan, dvs. på halva höjden).
När vi nu har kunnat ge nya tolkningar på de olika delarna kan vi se hela formeln i ett annat ljus. Vi kan läsa den på följande sätt: ytan = mittsektionens omkrets × den sluttande höjden.
Vi kommer då ihåg regeln för ett parallelltrapets: ytan = mittlinjen × höjden. (Mittlinjen ligger mitt emellan de två parallella sidorna av trapetset.) Om vi intuitivt ser analogin i dessa båda formuleringar om den stympade konen och om trapetset, kan vi se hela resultatet för den stympade konen "nästan direkt". Det vill säga, vi känner på oss att ett kort och direkt bevis av den lösning som vi kommit fram till genom en lång beräkning nu ligger inom räckhåll.
2. Ovanstående exempel är typiskt. Är vi inte helt tillfredsställda med härledningen av lösningen vill vi förbättra den, ändra den. Därför studerar vi lösningen och försöker förstå den bättre, försöker att se någon ny aspekt av den. Kanske lyckas vi först finna någon ny tolkning av en viss liten del i lösningen. Sedan kanske vi har turen att upptäcka ett nytt sätt att föreställa sig någon annan del.
Undersöker vi de olika delarna en efter en och försöker att se dem ur olika synvinklar, kommer vi kanske slutligen att kunna se hela resultatet i ett annorlunda ljus, och vår nya uppfattning av det kan leda till ett nytt bevis.
Det skall erkännas att allt detta antagligen oftare händer en erfaren matematiker som sysslar med något avancerat problem än en nybörjare som kämpar med ett elementärt problem. Matematikern som besitter en hel del kunskaper utsätts mer än nybörjaren för risken att med hjälp av alla sina kunskaper konstruera ett onödigt invecklat bevis. Men i stället är den erfarne matematikern i ett bättre läge än nybörjaren när det gäller att omtolka någon del av resultatet och att med hjälp av sådana små förändringar så småningom kunna formulera om hela lösningen.
Likväl kan det även på elementära stadier hända att eleverna presenterar en onödigt komplicerad lösning. Då bör läraren visa dem, åtminstone en eller två gånger, inte bara hur man skall lösa problemet på ett enklare sätt utan också hur man genom att granska resultatet kan hitta antydningar om en kortare lösning.
Se även Reductio ad absurdum och indirekt bevis.
Kan du kontrollera resultatet? Kan du kontrollera bevisföringen? Ett positivt svar på dessa frågor styrker vår tro på lösningen och bidrar till att befästa våra kunskaper.
1. Numeriska resultat till matematiska problem kan prövas genom att man jämför dem med observerade värden eller genom att man använder sunda förnuftet när man bedömer resultatet. Eftersom problem som uppstår ur praktiska behov eller av naturlig nyfikenhet nästan alltid handlar om fall från verkligheten skulle man kunna vänta sig att sådana bedömningar av anmärkningsvärda fakta inte försummas. Ändå vet varje lärare att elever åstadkommer otroliga saker i detta avseende. En del elever reagerar inte alls när de får resultatet 16 130 m som längden av en båt eller 8 år och 2 månader som åldern på kaptenen om vilken man för övrigt vet att han är farfar. Sådan vårdslöshet med det uppenbara tyder inte nödvändigtvis på dumhet utan i stället på likgiltighet för konstgjorda problemställningar.
2. Problem formulerade "i bokstäver" kan prövas på flera och mera intressanta sätt än problem formulerade "i siffror" (avsnitt 14). Låt oss som ytterligare exempel betrakta en stympad pyramid med kvadratisk bas. Om sidan av den undre basen är a, sidan av den övre basen b och höjden h finner vi att volymen är (a² + ab + b²)h/3. Vi kan pröva detta resultat genom Specialisering. Om t.ex. b = a övergår den stympade pyramiden i ett prisma och formeln ger a²h. Om b = 0 övergår den stympade pyramiden i en vanlig pyramid och formeln ger a²h/3. Vi kan också använda Dimensionstest. Vi ser då att formeluttrycket har dimensionen för kuben av en längd. Vi kan vidare testa formeln genom att variera de givna uppgifterna. Om någon av de positiva storheterna a, b eller h ökar så ser vi också att värdet av uttrycket ovan ökar.
Kontroller av detta slag kan tillämpas inte bara på det slutliga resultatet utan också på dellösningar. De är så värdefulla att det är mödan värt att tillämpa dem; se Variera problemet, 4. För att kunna använda sådana kontroller är det ibland fördelaktigt att generalisera ett problem formulerat "i siffror" till ett som är formulerat "i bokstäver"; se Generalisering, 3.
3. Kan du kontrollera bevisföringen? När vi kontrollerar vår argumentation steg för steg skall vi undvika att det blir blott och bart en repetition. För det första tenderar en repetition att bli långtråkig, intetsägande, en påfrestning för vår uppmärksamhet. För det andra är det sannolikt att vi kör fast igen på ett ställe där vi kört fast förut om omständigheterna är likadana som första gången. Om vi anser att det är nödvändigt att gå igenom hela bevisföringen igen steg för steg skall vi åtminstone ändra på ordningen mellan stegen eller på deras gruppering för att få variation.
4. Det är mera intressant och kräver mindre ansträngning att plocka ut bevisföringens svagaste punkt och undersöka den först. En fråga som är mycket användbar när det gäller att plocka ut punkter ur ett resonemang som är värda att undersöka är: Använde du alla de givna uppgifterna?
5. Det är självklart att våra icke-matematiska kunskaper inte kan vara helt baserade på formella bevis. Den mera gedigna delen av vår allmänbildning prövas och stärks ständigt genom våra vardagliga erfarenheter. Tester genom observation genomförs mer systematiskt inom naturvetenskaperna. Sådana tester utformas som noggranna experiment och mätningar och kombineras med matematiska resonemang inom de fysikaliska vetenskaperna. Kan våra kunskaper i matematik baseras enbart på formella bevis?
Detta är en filosofisk fråga som vi inte kan diskutera här. Helt säkert är att dina kunskaper eller mina kunskaper eller dina elevers kunskaper i matematik inte är baserade enbart på formella bevis. Om det finns några gedigna kunskaper över huvud taget så har de en bred experimentell bas, och denna bas breddas genom varje problem vars resultat prövas med framgång.
Korollarium (följdsats) är en sats som vi lätt finner som följd av en annan sats om vi undersöker denna. Ordet är av latinskt ursprung. En mer ordagrann översättning skulle vara "gåva" eller "belöning" eller "dricks".
Känner du till något närbesläktat problem? Vi kan knappast föreställa oss något problem som är absolut nytt, olikt allt annat och obesläktat med alla förut lösta problem. Om ett sådant problem existerade skulle det vara olösbart. I själva verket drar vi alltid nytta av tidigare lösta problem när vi löser ett nytt problem. Vi använder deras resultat eller deras metod eller den erfarenhet vi fick när vi löste dem. Och de problem vi drar nytta av måste naturligtvis på något sätt vara besläktade med det aktuella problemet. Därför frågan: Känner du till något närbesläktat problem?
Vanligtvis är det inte alls svårt att komma på tidigare lösta problem som är mer eller mindre besläktade med det aktuella. Det kan tvärtom dyka upp för många och vi kanske får svårt att välja ett som är användbart. Vi måste leta efter verkligt närbesläktade problem. Vi betraktar den obekanta eller vi söker ett tidigare löst problem som förenas med det aktuella genom Generalisering, Specialisering eller Analogi.
Den fråga som vi nu diskuterar syftar till att mobilisera våra tidigare förvärvade kunskaper (Framsteg och prestation, 1). En stor del av våra matematiska kunskaper ligger lagrad i form av tidigare bevisade satser. Därför frågan: Känner du till någon sats som skulle kunna användas? Denna fråga kan vara speciellt lämplig när vi har ett "bevisproblem", dvs. när vi måste bevisa eller vederlägga en given sats.
Leibniz, Gottfried Wilhelm (1646-1716), stor matematiker och filosof, planerade att skriva om "konsten att uppfinna" men han genomförde aldrig sin plan. Åtskilliga fragment som finns utströdda i hans arbeten visar emellertid att han hade intressanta idéer i detta ämne, vars betydelse han ofta framhävde. Så skrev han t.ex.: "Ingenting är viktigare än att kunna se källorna till upptäckter och uppfinningar. Det är, enligt min åsikt, intressantare än uppfinningarna själva."
Lemma betyder "hjälpsats". Ordet är av grekiskt ursprung. En mer bokstavlig översättning skulle lyda "det antagna".
Vi försöker bevisa en sats, låt oss kalla den A. Under arbetets gång kommer vi att förmoda att en annan sats, B, kanske är giltig. Om B vore sann skulle vi kanske kunna använda den för att bevisa A. Vi antar provisoriskt att B gäller, sparar beviset till senare och fortsätter i stället att bevisa A. En sådan antagen sats B kallas hjälpsats till den ursprungligen givna satsen A. Den här skildringen är ett ganska typiskt exempel och förklarar den nuvarande betydelsen av ordet lemma.
Ljus idé eller "god idé" eller "det går upp ett ljus" är vardagliga uttryck som beskriver ett plötsligt steg fram mot lösningen; se Framsteg och prestation, 6. Ljusa idéer har alla fått någon gång. Men det är svårt att beskriva vad en ljus idé är och därför kan det vara intressant att veta att en mycket målande beskrivning av den har gjorts i förbigående av en så gammal auktoritet som Aristoteles.
De flesta människor skulle hålla med om att en ljus idé formas i en "akt av skarpsinne". Aristoteles definierar "skarpsinne" på följande sätt: "Skarpsinne innebär att ögonblickligen med en gissning träffa på ett väsentligt samband. Om man t.ex. ser en person som talar med en rik man på ett speciellt sätt kan man kanske ögonblickligen gissa att denna person försöker låna pengar. Eller om man observerar att den ljusa sidan av månen alltid är vänd mot solen, kanske man plötsligen kommer till insikt om varför det är så; nämligen eftersom månen återstrålar solens ljus."|10|
Det första exemplet är inte dåligt men ganska trivialt. Det fordras inte mycket skarpsinne för att gissa sådana saker om rika personer och pengar, och idén är inte särskilt ljus. Det andra exemplet är emellertid mycket imponerande om vi bara tänker oss in i det sammanhang där det hör hemma.
Vi måste föreställa oss att en samtida till Aristoteles var tvungen att observera solen och stjärnorna om han ville bestämma tiden, eftersom det inte fanns några armbandsur. Eftersom det inte fanns någon gatubelysning var han tvungen att observera månens faser om han planerade att resa under natten. Han kände mycket bättre till himlen än en modern storstadsbo och hans naturliga intelligens var inte förvirrad av osmälta brottstycken från journalisters beskrivningar av astronomiska teorier. Han såg fullmånen som en flat skiva liknande solskivan men mycket mindre ljus. Han måste ha förundrat sig över de ständiga växlingarna i månens form och läge. Då och då observerade han månen också på dagen, vid soluppgång eller solnedgång, och kom fram till att "den ljusa sidan av månen alltid är vänd mot solen", vilket i sig själv var en aktningsvärd prestation. Och så upptäcker han att månen i detta avseende liknar en boll som belyses från ena sidan så att den ena halvan av den är ljus och den andra halvan mörk. Han föreställer sig solen och månen inte som flata skivor utan som runda kroppar, varav den ena ger och den andra reflekterar ljus. Han förstår det viktiga sambandet, han förändrar plötsligt sina tidigare föreställningar, "ögonblickligen". Det blir ett plötsligt föreställningssprång, han får en ljus idé, en snilleblixt.
Modern heuristik försöker att förstå processen att lösa problem, speciellt de tankeoperationer som normalt är användbara under denna process. Den utnyttjar olika kunskapskällor, av vilka ingen borde försummas. Ett allvarligt studium av heuristik måste därför ta hänsyn både till den logiska och den psykologiska bakgrunden. Våra studier får inte bortse från vad sådana äldre författare som Pappus, Descartes, Leibniz och Bolzano har att säga om ämnet, och de får minst av allt bortse från fördomsfri erfarenhet. Erfarenhet av att lösa problem och erfarenhet av att iaktta andra människor som löser problem måste vara den grund på vilken heuristiken är uppbyggd. När vi studerar får vi inte försumma något slag av problem, och vi bör försöka finna gemensamma drag i sättet att behandla alla slags problem. Vi bör försöka frilägga de allmänna dragen, de som är oberoende av problemets ämnesområde. Heuristisk forskning har "praktiska" syften. En bättre förståelse för de tankeoperationer som normalt är användbara vid problemlösning skulle kunna utöva ett gott inflytande på undervisningen, speciellt på matematikundervisning.
Föreliggande bok är ett första försök mot realiserandet av detta program. Vi skall nu diskutera hur de skilda artiklarna i detta Lexikon passar in i programmet.
1. Vår lista är i själva verket en lista på tankeoperationer som normalt är användbara när man löser problem. De angivna frågorna och uppmaningarna skall antyda sådana operationer. En del av dessa operationer beskrivs även i bokens andra del och några av dem diskuteras och illustreras mer utförligt i första delen.
För ytterligare belysning av olika frågor och uppmaningar på listan bör läsaren studera de 15 artiklar i vårt Lexikon, vars rubriker återger de första meningarna i listans 15 paragrafer: Vad är det som söks? Är det möjligt att uppfylla villkoret? Rita en figur … Kan du använda resultatet? Den läsare som önskar information om någon speciell detalj på listan bör titta på de första orden i paragrafen i fråga och sedan slå upp den artikel i Lexikonet som har dessa första ord som rubrik. Sålunda finner man t.ex. uppmaningen Gå tillbaka till definitionerna i den paragraf på listan vars första mening är: Skulle du kunna formulera om problemet? Under denna rubrik finner läsaren en hänvisning till Definition, där uppmaningen i fråga förklaras och illustreras.
2. Problemlösning är en komplicerad process som har åtskilliga olikartade aspekter. De tolv huvudartiklarna i detta Lexikon behandlar vissa av dessa aspekter något så när utförligt. Vi kommer att nämna ifrågavarande rubriker i det följande.
När vi arbetar koncentrerat känner vi intensivt hur arbetet framskrider. Vi blir förtjusta när framstegen går snabbt och modfällda när de går långsamt. Vad är väsentligt för Framsteg och prestation när man löser problem? Den artikel som tar upp denna fråga citeras ofta i andra delar av Lexikonet och bör läsas på ett ganska tidigt stadium.
När vi försöker lösa ett problem studerar vi olika aspekter av det i tur och ordning, vi vrider och vänder oupphörligt på det i vårt huvud. Att Variera problemet är nödvändigt för vårt arbete. Vi kan variera problemet genom Uppdelning och rekombinering av dess element eller genom att gå tillbaka till Definitionen av någon av dess termer eller vi kan använda de stora resurser som bjuds i Generalisering, Specialisering och Analogi. Variation av problemet kan leda oss till Hjälpkonstruktioner eller till upptäckten av ett mer tillgängligt Hjälpproblem.
Vi måste noga skilja mellan två olika slags problem, Sökproblem och Bevisproblem. Vår lista är speciellt anpassad för "sökproblem". Den måste revideras och några av dess frågor och uppmaningar ändras för att den skall vara tillämpbar också på "bevisproblem".
I alla slags problem och speciellt i matematiska problem som inte är alltför enkla spelar lämplig Notation och lämpliga geometriska Figurer en stor och ofta oumbärlig roll.
3. Processen att lösa problem har många aspekter men några av dem tas inte alls upp i denna bok och andra endast mycket kortfattat. Det är antagligen motiverat att i en första kort översikt utesluta sådana punkter som skulle te sig alltför subtila eller för tekniska eller för kontroversiella.
Provisorisk, enbart möjlig Heuristisk argumentation är viktig för att man skall kunna upptäcka en lösning, men man får aldrig ta den för ett bevis. Man måste gissa men också Granska gissningen. Arten av heuristiska argument diskuteras i Tecken på framsteg, men diskussionen skulle kunna fortsättas.
Betraktelsen av vissa logiska mönster är betydelsefull för vårt ämne men det har förefallit lämpligast att inte ta med någon teknisk artikel. Endast två artiklar behandlar huvudsakligen psykologiska aspekter, artiklarna Beslutsamhet, hopp, framgång och Det undermedvetna arbetet. En kommentar om djurpsykologi görs i förbigående i artikeln Att arbeta baklänges.
Det måste framhållas att alla slags problem, speciellt Praktiska problem och t.o.m. pussel och Ordgåtor, ligger inom heuristikens område. Det måste likaledes framhållas att osvikliga Regler för upptäckande ligger utom ramen för seriös forskning. Heuristiken diskuterar mänskligt beteende i samband med problem. Detta har förmodligen varit på modet sedan de första mänskliga samhällenas början.
4. En del artiklar rörande speciella frågor har tagits med och några avsnitt om mer generella aspekter har behandlats utförligare eftersom de, eller delar av dem, skulle kunna vara av speciellt intresse för elever eller lärare.
Metodiska frågor som ofta är av betydelse inom elementär matematik diskuteras i Pappus, Att arbeta baklänges, Reductio ad absurdum och indirekt bevis, Induktion och matematisk induktion, Att ställa upp ekvationer, Dimensionstest och Varför behövs bevis? En del artiklar vänder sig speciellt till lärare, såsom Rutinproblem och Diagnos, och andra vänder sig till elever som är något ambitiösare än genomsnittet, såsom Den intelligente problemlösaren, Den intelligente läsaren och Den blivande matematikern.
Det kan nämnas här att de dialoger mellan läraren och hans elever som ges i avsnitten 8, 10, 18, 19, 20 och i olika artiklar i Lexikonet kan tjäna som modell inte bara för läraren som försöker ge sin klass vägledning utan också för problemlösaren som arbetar på egen hand. Att beskriva tänkandet som "diskussion i tanken", som en sorts konversation mellan tänkaren och honom själv, är inte alls malplacerat. Dialogerna i fråga visar hur lösningen framskrider. Problemlösaren som talar med sig själv kan komma fram efter samma mönster.
5. Vi skall inte gå igenom de återstående rubrikerna utan bara nämna några få grupper.
Några artiklar innehåller kommentarer om vårt ämnes historia, om Descartes, Leibniz, Bolzano, om Heuristik, om Beteckningar och termer och om Pappus. Några få artiklar förklarar facktermer: Villkor, Korollarium, Lemma. Andra innehåller enbart hänvisningar (markeras med asterisk i innehållsförteckningen).
6. Heuristiken eftersträvar allmängiltighet, den studerar procedurer som är oberoende av ämnesområdet och som är tilllämpbara på alla slags problem. Föreliggande framställning anför emellertid nästan enbart elementära matematiska problem som exempel. Vi får inte glömma bort att detta innebär en begränsning, men författaren hoppas att denna begränsning inte allvarligt skall skymma tendensen i vårt ämne. Elementära matematiska problem uppvisar i själva verket all önskvärd variation, och studiet av deras lösning är speciellt lätttillgängligt och intressant. Dessutom är icke-matematiska problem inte helt bortglömda fastän de sällan anförs här som exempel. Mera avancerade matematiska problem förekommer aldrig direkt men utgör den reella bakgrunden till den föreliggande framställningen. Fackmatematikern som har intresse för denna typ av studium kan lätt lägga till exempel från sin egen erfarenhet för att ytterligare belysa punkter som här är illustrerade genom elementära exempel.
7. Författaren till denna bok vill gärna uttrycka sin tacksamhetsskuld till några moderna författare som inte finns med i artikeln om Heuristik. Dessa är fysikern och filosofen Ernst Mach, matematikern Jacques Hadamard, psykologerna William James och Wolfgang Köhler. Han vill också nämna psykologen K. Duncker och matematikern F. Krauss, vilkas arbeten (publicerade efter det att hans egna forskningar var tämligen framskridna och delvis publicerade) uppvisar vissa parallella iakttagelser.
Motsägelsefull. Se Villkor.
Notation. Om man vill få en uppfattning av fördelarna med en välvald och välkänd notation så kan man försöka addera några inte för små tal skrivna inte med de välkända arabiska siffrorna utan t.ex. med romerska siffror. Tag t.ex. talen MMMXC, MDXCVI, MDCXLVI, MDCCLXXXI och MDCCCLXXXVII.
Det är knappast möjligt att överskatta betydelsen av matematisk notation. Moderna elektroniska räknemaskiner som använder decimalsystemet har stora fördelar framför de äldre maskinerna som inte kunde skriva tal på detta bekväma sätt. En medelmåttig nutida elev som är van vid de vanliga beteckningssätten inom algebra, analytisk geometri och differential- och integralkalkyl har ett enormt övertag över en grekisk matematiker när det t.ex. gäller att lösa problem som handlar om ytor och volymer och som sysselsatte ett sådant geni som Arkimedes.
1. Att tala och att tänka är två processer som är nära förbundna med varandra. Användningen av ord stöder tanken. Vissa filosofer och filologer har gått ett steg längre och menar att användningen av ord är absolut nödvändig för att man skall kunna bruka förnuftet.
Det sista påståendet kan likväl tyckas något överdrivet. Den som har någon erfarenhet av allvarligt matematiskt arbete vet att man kan tänka skarpt utan att använda ord enbart genom att betrakta geometriska figurer eller manipulera med algebraiska symboler. Figurer och symboler är nära förknippade med matematiskt tänkande. De stöder tanken. Vi skulle kunna förbättra filosofernas och filologernas något snäva påstående genom att placera ord på samma nivå som alla andra slag av tecken och säga att bruk av tecken förefaller oumbärligt för att man skall kunna bruka förnuftet.
Hur som helst liknar användningen av matematiska symboler användningen av ord. Matematisk notation verkar som ett slags språk, une langue bien faite, ett språk väl anpassat för sitt ändamål, koncist och precist, med regler som i motsats till vanliga grammatiska regler inte har några undantag.
Att ställa upp ekvationer innebär, om vi accepterar detta synsätt, ett slags översättning, en översättning från vanligt språk till de matematiska symbolernas språk.
2. Några matematiska symboler som + och -, = och åtskilliga andra har en fastställd traditionell betydelse, medan andra symboler, såsom små och stora bokstäver i romerska eller grekiska alfabetet, används i skilda betydelser i olika sammanhang. När vi ställs inför ett nytt problem måste vi välja vissa symboler, vi måste införa lämpliga beteckningar. Det finns någonting analogt i användningen av vanligt språk. Många ord används i olika betydelser beroende på sammanhanget. Där det är nödvändigt med precision måste vi välja våra ord omsorgsfullt.
Ett betydelsefullt steg i problemlösning är att välja beteckningar. Detta skall göras med omsorg. Den tid vi nu lägger ner på att välja lämpliga beteckningar kan mycket väl betala sig genom att vi senare sparar tid därigenom att vi undviker tveksamhet och otydlighet. Att ägna omsorg åt notationen innebär dessutom att vi måste tänka igenom de olika element i problemet som skall betecknas med någonting. På så sätt kan valet av lämpliga beteckningar väsentligt bidra till att vi förstår problemet.
3. En god notation skall vara otvetydig, koncis, lätt att komma ihåg. Den får inte innehålla olämpliga undermeningar men kan utnyttja användbara undermeningar. Ordningen och sambandet mellan tecknen skall antyda ordningen och sambandet mellan objekten i fråga.
4. Tecken och symboler måste framför allt vara otvetydiga. Det får inte förekomma att samma symbol betecknar två skilda element i samma undersökning. Om man kallar en viss storhet a när man löser ett problem skall man undvika att beteckna någonting annat med a som hänger ihop med samma problem. Naturligtvis kan man använda bokstaven a i en annan mening i ett helt annat problem.
Även om man inte skall använda samma symbol för skilda objekt kan man mycket väl använda olika symboler för samma objekt. Så kan t.ex. produkten av a och b skrivas som a × b, a · b eller ab. I en del fall kan det vara lämpligt att använda två eller flera olika symboler för samma objekt, men sådana fall kräver särskild omsorg. Vanligtvis är det bättre att använda bara en symbol för ett objekt och under inga omständigheter får flera symboler användas på ett godtyckligt sätt.
5. En bra symbol skall vara lätt att komma ihåg och lätt att känna igen. Symbolen bör omedelbart påminna oss om objektet och objektet om symbolen.
En enkel teknik för att göra symboler lätt igenkännbara är att använda initialer. I avsnitt 20 använde vi t.ex. u för utströmningshastigheten, t för tiden, V för volymen. Vi kan emellertid inte alltid använda initialer, kanske helt enkelt av den anledningen att några redan är upptagna. Det finns också andra skäl som begränsar valet av symboler och andra medel att göra dem lätt igenkännliga som vi nu skall diskutera.
6. Notationen är inte bara lätt igenkännlig utan också till stor hjälp för vår föreställning om ett problem såvida ordningen och sambandet mellan tecknen antyder ordningen och sambandet mellan objekten. Vi behöver fler exempel för att illustrera denna punkt.
a) För att beteckna objekt som begreppsmässigt ligger nära varandra i ett problem använder vi bokstäver som ligger nära varandra i alfabetet.
I allmänhet använder vi därför bokstäver i början av alfabetet, t.ex., a, b, c, för givna storheter eller konstanter och bokstäver i slutet av alfabetet, t.ex. x, y, z, för okända storheter eller variabler.
I avsnitt 8 använde vi a, b, c för den givna längden, bredden och höjden i en parallellepiped. I detta fall var beteckningarna a, b, c att föredra framför initialerna l, b, h. De tre sträckorna spelade samma roll i problemet, vilket understryks genom användning av på varandra följande bokstäver. Dessutom är bokstäverna a, b, c som vi just antydde de vanligaste bokstäverna för att beteckna givna storheter. Vid något annat tillfälle, då de tre sträckorna spelar olika roll och det är viktigt att veta vilken sträcka som är horisontell och vilken som är vertikal, kan beteckningarna 1, b, h vara att föredra.
b) För att beteckna objekt tillhörande en viss kategori använder vi vanligtvis bokstäver tillhörande samma alfabet för en kategori och använder olika alfabet för olika kategorier. I plan geometri använder vi t.ex. ofta
Om vi har två objekt som hör till skilda kategorier men som står i viss relation till varandra av betydelse för problemet, kan vi för att beteckna dessa två objekt välja motsvarande bokstäver inom resp. alfabet såsom A och a, B och b osv. Ett välkänt exempel är den vanliga notationen för elementen i en triangel:
Det är då underförstått att a är den sida som står mot hörnet A och att vinkeln vid A kallas α.
c) I avsnitt 20 är bokstäverna a, b, x, y särskilt lämpliga för att ange arten av och sambandet mellan de angivna elementen. Bokstäverna a, h antyder att storheterna är konstanta, x, y betecknar variabler, a föregår b på samma sätt som x föregår y och detta antyder att a står i samma relation till b som x till y. I själva verket är a och x horisontella, b och y vertikala, och vi har att a : b = x : y.
7. Beteckningssättet ΔABC ~ Δ EFG innebär att de två trianglarna i fråga är likformiga. I moderna böcker innebär formeln att trianglarna är likformiga och att deras hörn motsvarar varandra i den ordning som de är skrivna, A mot E, B mot F, C mot G. I äldre böcker där denna regel ännu inte var införd måste läsaren titta på figuren eller komma ihåg härledningen för att vara säker på vilket hörn som motsvarade vilket.
Det nya beteckningssättet är mycket bättre och elegantare. Om vi använder modern notation kan vi dra slutsatser ur sambandet utan att titta på figuren. Så kan vi t.ex. sluta oss till att ![]() A =
A = ![]() E, AB:BC = EF:FG m.m. av samma slag. Den äldre notationen uttrycker mindre och tillåter inte sådana bestämda slutsatser.
E, AB:BC = EF:FG m.m. av samma slag. Den äldre notationen uttrycker mindre och tillåter inte sådana bestämda slutsatser.
Ett beteckningssätt som uttrycker mer än ett annat kan kallas för mer pregnant. Det moderna sättet att beteckna likformighet för trianglar är mer pregnant än det äldre. Det återspeglar ordningen och sambandet mellan objekten mera fullständigt än det äldre och det kan därför utgöra grund för flera slutsatser än det äldre.
8. Ord har ibland en undermening. Vissa sammanhang i vilka ett ord ofta används påverkar ordet och lägger till någonting till dess egentliga betydelse, någon nyans eller undermening eller bibetydelse. Om vi uttrycker oss omsorgsfullt försöker vi att av de ord som alla har nästan samma betydelse välja ut det vars undermening passar bäst.
Något liknande gäller för matematiska beteckningar. Även matematiska symboler kan få ett slags undermening genom de sammanhang i vilka de ofta används. Om vi vill välja beteckningarna noga måste vi ta hänsyn till denna omständighet. Låt oss illustrera detta.
Det finns vissa bokstäver som har förvärvat en fast rotad, traditionell betydelse. Så betecknar t.ex. e vanligen basen för de naturliga logaritmerna, i betecknar √-l, den imaginära enheten, och π betecknar förhållandet mellan omkrets och diameter i en cirkel. I allmänhet är det bäst att använda sådana symboler enbart i deras traditionella betydelse. Om vi använder en sådan symbol i någon annan betydelse skulle den traditionella betydelsen ibland kunna verka störande och t.o.m. vilseledande. Som regel förorsakar olämpliga undermeningar av detta slag mindre besvär för nybörjaren, som ännu inte har studerat så många ämnen, än för matematikern som borde ha tillräcklig erfarenhet för att komma tillrätta med sådana olägenheter.
Symbolernas bibetydelser kan också vara nyttiga, t.o.m. mycket nyttiga, om de används med förstånd. En beteckning som använts vid tidigare tillfällen kan hjälpa oss att komma ihåg någon användbar metod. Naturligtvis måste vi vara noga med att klart skilja den nuvarande (primära) betydelsen hos symbolen från dess förra (sekundära) betydelse. Ett stående beteckningssätt [som den traditionella notationen för elementen i en triangel, omnämnd i avsnitt 6 b] har stora fördelar. Sedan det använts vid flera tidigare tillfällen kan det hjälpa oss att komma ihåg olika förut använda procedurer. Vi kommer ihåg våra formler uttryckta enligt något stående beteckningssätt. Naturligtvis måste vi då se upp när vi på grund av speciella omständigheter tvingas använda stående beteckningar i en mening som avviker från den vanliga.
9. När vi måste välja mellan två beteckningssätt kan ett skäl tala för det ena och något annat skäl för det andra. Vi behöver erfarenhet och omdöme för att välja det lämpligaste sättet precis som vi behöver erfarenhet och omdöme för att välja de lämpligaste orden. Ändå kan det vara bra att veta de olika fördelar och nackdelar som diskuterats i det föregående. I alla händelser bör vi välja notationen omsorgsfullt och ha ett gott skäl för vårt val.
10. Inte bara de mest hopplösa elever utan även mycket intelligenta elever kan känna en aversion mot algebra. Det ligger alltid någonting godtyckligt och konstlat i notation. Att lära ett nytt beteckningssätt är en belastning för minnet. Den intelligente eleven kan vägra att ta detta besvär om han inte ser att han får något utbyte av det. Han kan ha helt rätt i sin aversion mot algebra om han inte ges en verklig chans att genom egen erfarenhet övertyga sig om att det matematiska symbolspråket hjälper tänkandet. Att hjälpa eleven att göra sådana erfarenheter är en viktig uppgift för varje lärare, kanske en av hans mest betydelsefulla uppgifter.
Uppgiften är betydelsefull men därmed är inte sagt att den är lätt. Ovanstående kommentarer kan kanske vara till någon hjälp. Se även Att ställa upp ekvationer. Att kontrollera en formel genom en utförlig diskussion av dess egenskaper kan rekommenderas som en speciellt lärorik övning. Se avsnitt 14 och Kan du kontrollera resultatet?, 2.
Om du inte kan lösa det givna problemet så låt inte detta misslyckande plåga dig för mycket. Försök trösta dig med någon lättare framgång, försök först lösa något liknande problem. Därefter kanske du finner mod att angripa det ursprungliga problemet igen. Glöm inte att människans överlägsenhet består i att hon kan gå runt ett hinder som inte kan övervinnas direkt, i att hon kan komma på något lämpligt hjälpproblem när det ursprungliga problemet verkar olösligt.
Kan du komma på något närbesläktat problem som är lättare att angripa? Du skall nu hitta på, uppfinna ett närbesläktat problem, inte enbart komma ihåg ett. Jag förutsätter att du redan har försökt frågan: Känner du till något närbesläktat problem?
De övriga frågorna i den paragraf på listan som börjar med rubriken på den här artikeln har ett gemensamt syfte, att Variera problemet. Det finns olika metoder att nå detta syfte, såsom Generalisering, Specialisering, Analogi och andra som innebär olika sätt till Uppdelning och rekombinering.
Ordgåtor. Enligt avsnitt 3 är frågorna och uppmaningarna på vår lista oberoende av ämnesområde och tillämpbara på alla slags problem. Det kan vara intressant att se om detta påstående håller genom att betrakta några ordgåtor.
Ta t.ex. orden DRY OXTAIL IN REAR.|11| Problemet är att finna ett anagram, dvs. ett enda ord erhållet genom omkastning av bokstäverna. Det är intressant att lägga märke till att när vi löser denna ordgåta så är åtskilliga frågor på listan både relevanta och stimulerande.
Vad är det som söks? Ett ord.
Vad är det som är givet? De fyra orden DRY OXTAIL IN REAR.
Hur lyder villkoret? Det sökta ordet har 15 bokstäver, nämligen bokstäverna i de givna fyra orden. Det handlar förmodligen om ett inte alltför ovanligt engelskt ord.
Rita en figur. Det kan vara lämpligt att markera 15 tomma platser:
---------------
Skulle du kunna formulera om problemet? Vi skall finna ett ord som innehåller bokstäverna A A E I I O Y D L N R R R T X ordnade på ett visst sätt.
Detta är otvivelaktigt en ekvivalent omformulering av problemet (se Hjälpproblem, 6). Det kanske är en användbar omformulering. Genom att skilja vokalerna från konsonanterna (detta är viktigt, alfabetisk ordning ger ingenting) kan vi se en annan aspekt av problemet. Vi ser nu nämligen att det sökta ordet har sju stavelser såvida det inte innehåller några diftonger.
Om du inte kan lösa det givna problemet, försök först lösa något liknande problem. Ett besläktat problem är att forma ord med bara några av de givna bokstäverna. Vi kan naturligtvis skapa sådana korta ord. Sedan försöker vi finna längre och längre ord. Ju fler bokstäver vi använder, ju närmare kommer vi det sökta ordet.
Skulle du kunna lösa en del av problemet? Det sökta ordet är så långt att det måste ha mindre, klart särskiljbara delar. Det är förmodligen ett sammansatt ord eller också är det härlett från något annat ord genom att någon vanlig ändelse har lagts till. Vilken vanlig ändelse skulle det kunna vara?
Behåll endast en del av villkoret, förkasta den andra delen. Vi kan nu försöka komma på ett långt ord eventuellt med så många som sju stavelser och relativt få konsonanter och som innehåller ett X och ett Y.
Frågorna och uppmaningarna på vår lista kan inte hjälpa oss att trolla. De kan inte ge oss lösningen till alla möjliga ordgåtor utan någon ansträngning från vår sida. Om läsaren vill finna ordet måste han fortsätta att grubbla på det och försöka om och om igen. Vad frågorna och uppmaningarna på listan kan göra är att "hålla bollen rullande". Om vi blir benägna att släppa problemet när vi inte tycks komma vidare, kan de få oss att göra ett nytt försök eller visa oss en ny aspekt, en ny variant av problemet, ge oss ny stimulans. De kan få oss att fortsätta tänka.
För ytterligare exempel se Uppdelning och rekombinering, 8.