SYFTE
1. Att hjälpa eleven. En av de viktigaste uppgifterna för en lärare är att hjälpa sina elever. Denna uppgift är inte alldeles lätt. Den kräver tid, övning, hängivenhet och sunda principer.
Eleven bör skaffa sig så mycket erfarenhet av självständigt arbete som möjligt. Men om han lämnas ensam med sitt problem utan hjälp eller med otillräcklig hjälp kanske han inte gör några framsteg alls. Om läraren hjälper för mycket lämnar han ingenting till eleven. Läraren bör hjälpa, men inte för mycket och inte för litet, för att eleven skall få en rimlig del i arbetet.
Om eleven inte förmår göra mycket på egen hand bör läraren åtminstone ge honom en illusion av självständigt arbete. För att lyckas med detta måste läraren hjälpa eleven diskret och försynt.
Det bästa är emellertid att hjälpa eleven på ett sätt som är naturligt. Läraren måste försätta sig i elevens situation. Han måste se fallet som eleven upplever det. Han måste försöka förstå vad som pågår i elevens huvud och ställa en fråga eller antyda ett steg som eleven skulle ha kunnat komma på själv.
2. Frågor, rekommendationer, tankeoperationer. När läraren försöker hjälpa eleven på ett effektivt men försynt och naturligt sätt, föranleds han att ställa samma frågor och antyda samma steg och åtgärder om och om igen. Så måste man t.ex. i otaliga problem ställa frågan: Vad är det som söks? Vi kan variera orden och fråga samma sak på många olika sätt: Vad skall vi räkna ut? Vad är det vi önskar finna? Vad är det som är okänt? Avsikten med dessa frågor är att koncentrera elevens uppmärksamhet på den okända storheten. Ibland uppnår vi samma effekt mer naturligt med en uppmaning: Betrakta den obekanta! Fråga och uppmaning syftar till samma effekt. De vill provocera fram samma tankeoperation.
Författaren har ansett det vara mödan värt att samla och gruppera frågor och uppmaningar som normalt är användbara när man diskuterar problem med elever. Den lista vi studerar innehåller omsorgsfullt valda och ordnade frågor och uppmaningar av detta slag. De är lika användbara för en problemlösare som arbetar ensam. Om läsaren är tillräckligt förtrogen med listan så att han bakom uppmaningen kan se vilken reell åtgärd som föreslås, kommer han att upptäcka att listan indirekt räknar upp tankeoperationer som normalt är användbara vid problemlösning. Dessa operationer är upptagna på listan i den ordning som de sannolikt kommer att utföras.
3. Allmängiltighet är en betydelsefull kvalitet som karakteriserar frågorna och uppmaningarna på listan. Ta frågorna: Vad är det som söks? Vad är det som är givet? Hur lyder villkoret? Dessa frågor är allmänt tillämpbara. Vi kan ställa dem med god effekt när vi behandlar alla slags problem. Deras användning är inte begränsad till något visst ämnesområde. Vårt problem kan vara algebraiskt eller geometriskt, matematiskt eller icke-matematiskt, teoretiskt eller praktiskt, ett seriöst problem eller enbart ett pussel - det spelar ingen roll. Frågorna är meningsfulla och kan hjälpa oss att lösa problemet.
Det finns faktiskt en begränsning, men den har ingenting att göra med ämnesområdet. Vissa frågor och uppmaningar på listan är endast tillämpbara på "sökproblem" (problem i vilket något söks, efterfrågas, ofta t.ex. värdet av en viss variabel), inte på "bevisproblem". Om vi har ett problem av det senare slaget måste vi använda frågor som är något annorlunda, se Sökproblem, Bevisproblem.
4. Sunt förnuft. Frågorna och uppmaningarna eller förslagen på vår lista är allmängiltiga, men förutom att vara allmängiltiga är de också naturliga, enkla, uppenbara, och härstammar ur vanligt sunt förnuft. Ta uppmaningen Betrakta den obekanta! Försök finna ett känt problem med samma eller liknande obekanta storhet. Denna uppmaning råder dig att göra vad du tänkte göra i vilket fall som helst, utan något råd, förutsatt att du är allvarligt engagerad i ditt problem. Är du hungrig? Du vill ha mat och du tänker på kända metoder att få tag på föda. Har du problem med en geometrisk konstruktion? Du vill konstruera en triangel och du tänker på en känd metod att konstruera trianglar. Har du problem av vilket slag som helst? Du vill finna en viss obekant storhet och du tänker på välbekanta metoder för att finna en sådan storhet eller någon liknande storhet. Om du gör detta följer du exakt den uppmaning vi citerade från listan. Och du är på rätt spår dessutom. Förslaget är bra, det uppmanar dig att försöka med en procedur som ofta visat sig vara framgångsrik.
Alla frågor och uppmaningar på listan är naturliga, enkla, uppenbara, helt enkelt vanligt sunt förnuft. Men de formulerar vanligt sunt förnuft i allmänna ordalag. De uppmanar en person att företa sig det som förefaller naturligt för honom om han är allvarligt intresserad av sitt problem och har en del sunt förnuft. Men en person som uppför sig på det rätta sättet bryr sig vanligtvis inte om att uttrycka sitt beteende i klara ord, och det är möjligt att han inte skulle kunna göra det. Vår lista är ett försök att åstadkomma detta.
5. Lärare och elev. Att härma och öva. Läraren kan ha två föresatser i sinnet när han riktar en av frågorna eller uppmaningarna på listan till sina elever. För det första att hjälpa eleverna att lösa problemet i fråga. För det andra att utveckla elevernas förmåga så att de själva skall kunna lösa problem i framtiden.
Erfarenheten visar att frågorna och uppmaningarna på listan ofta hjälper en elev om de används på rätt sätt. De har två gemensamma kännetecken, sunt förnuft och allmängiltighet. Eftersom de härstammar ur sunt förnuft uppträder de ofta på ett naturligt sätt. Eleven skulle kunna ha kommit på dem själv. Eftersom de är allmängiltiga hjälper de på ett försynt sätt. De endast antyder en allmän riktlinje och lämnar massor för eleven att göra själv.
Men de två föresatser som nämndes ovan har ett klart sammanhang. Om eleven lyckas lösa problemet i fråga lägger han till en del till sin förmåga att lösa problem över huvud taget. Därför skall vi inte glömma att våra frågor är generella och tillämpbara i många fall. Om samma fråga gång på gång visar sig användbar kommer eleven knappast att kunna undgå att lägga märke till detta, och han kommer att ställa frågan till sig själv senare i en liknande situation. Ställer han frågan gång efter annan kanske han en gång lyckas få fram den rätta idén. Genom en sådan framgång upptäcker han det riktiga sättet att använda frågan, och därmed har han verkligen införlivat den i sitt tänkande.
En elev kan bli så väl förtrogen med en del frågor på listan att han till slut kan ställa den rätta frågan till sig själv i det rätta ögonblicket och utföra motsvarande tankeoperation målmedvetet och självklart. En sådan elev har naturligtvis fått ut det mesta möjliga av listan. Vad kan en lärare göra för att uppnå detta resultat?
Problemlösning är en praktisk verksamhet i likhet med t.ex. simning. Vi förvärvar allt slags praktisk skicklighet genom att härma, imitera och därefter öva och praktisera. När man försöker simma härmar man vad andra människor gör med sina händer och fötter för att hålla sitt huvud ovanför vattnet, och slutligen lär man sig simma genom att träna och praktisera. När man försöker lösa problem måste man observera och imitera vad andra människor gör när de löser problem, och slutligen lär man sig lösa problem genom att arbeta med dem.
Den lärare som vill utveckla sina elevers förmåga att lösa problem måste gradvis öka deras intresse för problem och ge dem rikligt med tillfällen att härma och öva. Om läraren hos sina elever vill framkalla de tankeoperationer som motsvarar listans frågor och uppmaningar, måste han använda dessa frågor och uppmaningar på eleverna så ofta det faller sig naturligt att göra det. Dessutom bör läraren dramatisera sina idéer något när han löser ett problem framför sina elever, och han bör ställa samma frågor till sig själv som han använder när han hjälper eleverna. Genom sådan ledning kommer eleven förr eller senare att upptäcka den rätta användningen av dessa frågor och uppmaningar, och när han gör det kommer han att förvärva någonting som betyder mer än kännedom om något särskilt matematiskt faktum.
INDELNING, KÄRNFRÅGOR
6. Fyra faser. När vi försöker finna en lösning kan vi hela tiden ändra angreppspunkt, ändra vårt sätt att betrakta problemet. Vi måste gång på gång ändra våra positioner. Vår uppfattning av problemet är sannolikt ganska ofullständig när vi börjar arbetet. Vår överblick förändras när vi gör något framsteg, den är annorlunda igen när vi är nästan framme vid lösningen.
För att gruppera frågorna och uppmaningarna på listan på ett lämpligt sätt skall vi särskilja fyra faser i arbetet. För det första måste vi förstå problemet. Vi måste se klart vad som erfordras. För det andra måste vi inse hur de olika delarna hänger ihop med varandra, hur det som söks är relaterat med det som är givet för att vi så skall kunna komma fram till en idé om hur lösningen skall se ut, för att vi alltså skall kunna göra en plan. För det tredje måste vi genomföra vår plan. För det fjärde måste vi se tillbaka på den färdiga lösningen, granska den och diskutera den.
Var och en av dessa faser har sin betydelse. Naturligtvis kan det inträffa att en elev direkt får en lysande idé och kastar fram lösningen utan några som helst förberedelser. Sådana snilleblixtar är visserligen i högsta grad önskvärda, men något icke önskvärt och olyckligt kan bli följden om eleven hoppar över någon av de fyra faserna utan att ha en bra idé. Det värsta kan inträffa om han tar itu med beräkningar eller konstruktioner utan att ha förstått problemet. Vanligtvis är det meningslöst att börja arbeta med detaljer utan att man har sett de stora sammanhangen, utan att man har gjort något slags plan. Många misstag skulle kunna undvikas om eleven, när han gör denna plan, kontrollerar varje steg i den. Några av de finaste effekterna kan gå förlorade om eleven inte bryr sig om att gå tillbaka och på nytt pröva den fullbordade lösningen.
7. Att förstå problemet. Det är dumt att svara på en fråga som man inte har förstått. Det är ledsamt att arbeta mot ett mål som man inte känner någon strävan att nå. Sådana dumma och ledsamma saker händer ofta, i och utanför skola och universitet, men en lärare måste försöka förhindra att sådant händer i hans klass. Eleverna måste förstå problemet. Men de bör inte bara förstå det, de bör också känna en önskan att kunna lösa det. Om en elev inte riktigt förstår ett problem eller saknar intresse för det är det inte alltid hans fel. Problemet måste vara väl valt, inte för svårt och inte för lätt, naturligt och intressant, och tid måste anslås för att ge det en naturlig och intressant presentation.
Framför allt måste framställningen av problemet vara begriplig. Läraren kan kontrollera detta till en viss grad. Han kan be eleverna upprepa formuleringen, och de skall kunna göra detta utan att tveka. En elev måste också kunna peka på problemets huvuddelar, på den okända storheten, på de givna storheterna, på villkoret. Läraren kan därför sällan utelämna frågorna: Vad är det som söks? Vad är det som är givet? Hur lyder villkoret?
Eleven bör noggrant betrakta huvuddelarna i problemet, flera gånger och från olika sidor. Om en figur hör till problemet bör han rita en figur och i denna ange den okända storheten och de givna storheterna. Om det är nödvändigt att namnge de olika elementen bör han införa lämpliga beteckningar. För att kunna fastställa lämpliga symboler tvingas han studera de element för vilka han skall välja symboler. Det finns en annan fråga som ofta är användbar i detta förberedande stadium, förutsatt att vi inte väntar något definitivt utan bara ett provisoriskt svar, en gissning: Är det möjligt att uppfylla villkoret?
(I den framställning som ingår i del 2, är avsnittet "Att förstå problemet" uppdelat i två avdelningar, "Att bli bekant med problemet" och "Att bättre förstå problemet".)
8. Exempel. Låt oss illustrera några av punkterna i föregående avsnitt. Vi väljer följande enkla problem: Sök diagonalen i en rektangulär parallellepiped vars längd, höjd och bredd är givna.
För att kunna diskutera detta problem på ett meningsfullt sätt måste eleverna känna till Pytagoras sats och några av dess tillämpningar i plan geometri, men de kan mycket väl ha obetydliga kunskaper i rymdgeometri. Läraren kan här utgå från elevens naturliga förtrogenhet med rumsliga relationer.
Läraren kan göra problemet intressant genom att konkretisera det. Klassrummet är en rektangulär parallellepiped vars dimensioner kan mätas och beräknas. Eleverna kan då försöka beräkna, eller "indirekt mäta", klassrummets diagonal. Läraren pekar ut klassrummets längd, bredd och höjd, dess diagonal antydd med en gest, och han kan göra figuren som han ritar på tavlan levande genom att då och då referera till klassrummet.
Dialogen mellan lärare och elever kan kanske börja på följande sätt:
"Längden av diagonalen i en parallellepiped."
"Vad är det som är givet?"
"Parallellepipedens längd, bredd och höjd."
"Inför lämpliga beteckningar. Vad skall vi kalla den okända storheten?"
"x"
"Vilka bokstäver skulle ni välja för längden, bredden och höjden?"
"a, b, c"
"Hur lyder villkoret som förenar a, b, c och x?"
"x är diagonalen i en parallellepiped vars längd, bredd och höjd är a, b och c."
"Är problemet rimligt? Jag menar, är villkoret tillräckligt för att bestämma den obekanta storheten?"
"Ja, det är det. Om vi känner a, b och c känner vi parallellepipeden. Om parallellepipeden är bestämd, är också diagonalen bestämd."
9. Att göra upp en plan. Vi har en plan när vi åtminstone i stora drag vet vilka beräkningar eller konstruktioner vi måste utföra för att finna den obekanta storheten. Vägen kan vara lång och mödosam från det att vi förstår problemet till dess att vi kan göra upp en plan. I själva verket ligger huvudprestationen i lösningen till ett problem i att komma på idén till en plan. Idén kan växa fram så småningom. Den kan också uppträda plötsligt, som en blixt, som en "ljus idé", efter synbarligen misslyckade försök och perioder av tvekan. Det bästa en lärare kan göra för eleven är att på ett diskret sätt förse honom med en ljus idé. De frågor och uppmaningar som vi kommer att diskutera är avsedda att framkalla en sådan idé.
För att kunna sätta sig in i elevens situation måste läraren tänka på sin egen erfarenhet, på sina egna svårigheter och framgångar när han löser problem.
Vi vet naturligtvis att det är svårt att komma på en god idé om vi har vaga kunskaper om ett ämne, och helt omöjligt om vi inte känner till någonting alls om det. Goda idéer bygger på erfarenhet och tidigare förvärvade kunskaper. Att enbart komma ihåg räcker inte för en god idé, men vi kan aldrig få någon god idé utan att dra oss till minnes vissa relevanta fakta. Enbart byggnadsmaterial räcker inte för att bygga ett hus, men vi kan inte bygga huset utan att skaffa det nödvändiga materialet. Det material som behövs för att lösa matematiska problem består av vissa relevanta detaljer bland våra tidigare förvärvade matematiska kunskaper, såsom tidigare lösta problem eller tidigare bevisade satser. Därför kan det ofta vara lämpligt att börja arbetet med frågan: Känner du till något närbesläktat problem?
Svårigheten är att det vanligtvis finns alldeles för många problem som på något sätt är besläktade med det aktuella, dvs. som - har någon del gemensam med det. Hur skall vi kunna välja ut det enda eller de få som verkligen är användbara just nu? Det finns då en uppmaning som sätter fingret på en väsentlig gemensam punkt: Betrakta den obekanta! Försök finna ett känt problem med samma eller liknande obekanta storhet.
Om vi lyckas komma på ett tidigare löst problem som är nära besläktat med det aktuella problemet har vi tur. Vi borde då försöka att vara förtjänta av en sådan tur. Vi förtjänar den om vi utnyttjar den. Här är ett närbesläktat problem som är löst förut. Skulle du kunna använda det?
Om de föregående frågorna tas på allvar och förstås rätt kan de ofta hjälpa oss i riktning mot de rätta idéerna, men de hjälper inte alltid. De kan inte trolla. Om de inte har någon effekt måste vi se oss om efter någon annan lämplig angreppspunkt och undersöka problemets olika aspekter. Vi måste variera, transformera, modifiera problemet. Skulle du kunna formulera om problemet? Några av frågorna på listan antyder särskilda metoder för att variera problemet, såsom generalisering, specialisering, användning av analogier, förkastande av en del av villkoret osv. Detaljerna är viktiga, men vi kan inte gå in på dem nu. En variation av problemet kan leda till något lämpligt hjälpproblem: Om du inte kan lösa det givna problemet, försök först lösa något liknande problem.
När man försöker utnyttja olika kända problem eller satser, betraktar olika modifieringar, experimenterar med olika hjälpproblem, kan man hamna så långt från det ursprungliga problemet att man löper risk att förlora det helt och hållet. Då finns det en bra fråga som kan föra oss tillbaka till det: Använde du alla de givna uppgifterna? Använde du hela villkoret?
10. Exempel. Vi återvänder till det exempel som vi studerade i avsnitt 8. När vi lämnade det hade eleverna just lyckats förstå innebörden av problemet och visade ett visst, svalt intresse för det. De skulle nu kunna ha några egna idéer eller ta egna initiativ. Om den uppmärksamme läraren ändå inte kan iaktta några tecken på sådana initiativ måste han omsorgsfullt sammanfatta dialogen med eleverna. Han måste vara beredd att med några modifieringar upprepa de frågor som eleverna inte svarade på. Han måste vara beredd att ofta mötas av en nedslående tystnad från elevernas sida (en tystnad som här kommer att antydas med punkter …).
"Känner ni till något närbesläktat problem?"
…
"Betrakta den obekanta! Känner ni till något problem som har samma obekanta storhet?"
…
"Nå, vad är det som söks?"
"Diagonalen i en parallellepiped."
"Känner ni till något problem med samma obekanta? "
"Nej. Vi har aldrig gått igenom någonting om diagonalen i en parallellepiped."
"Känner ni till något problem med en liknande obekant storhet?"
…
"Diagonalen är ett segment, en del av en rät linje. Har ni aldrig löst något problem där man sökte längden av en rät linje?"
"Jo visst, vi har löst sådana problem. T.ex. att finna sidan i en rät triangel."
"Bra! Här är ett närbesläktat problem som är löst förut. Skulle ni kunna använda det?"
…
"Ni hade turen att erinra er ett problem som är besläktat med det vi håller på med och som ni redan har löst. Skulle ni vilja utnyttja det? Skulle ni kunna införa någon hjälpkonstruktion så att ni kan använda det?"
…
"Titta här! Det problem ni kom på handlar om en triangel. Finns det någon triangel i den här figuren?"
| Fig.1 | 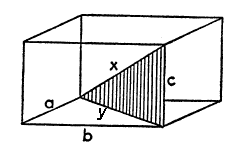 |
Låt oss hoppas att den sista ledtråden var tydlig nog att provocera fram lösningens idé, som består i att man inför en rät triangel (framhävd i fig. 1) i vilken den sökta diagonalen är hypotenusan. Ändå måste läraren vara beredd på att t.o.m. en sådan här uttrycklig ledtråd kan vara otillräcklig för att väcka eleverna ur deras dvala, och han måste vara beredd att använda en hel skala av alltmer tydliga ledtrådar och råd.
"Skulle ni vilja ha en triangel i den här figuren?"
"Vilket slags triangel skulle ni vilja ha i den här figuren?"
"Ni kan inte finna diagonalen än. Men ni sade att ni kunde finna sidan i en triangel. Hur förbättrar det saken?"
"Skulle ni kunna finna diagonalen om den vore en sida i en triangel?"
När eleverna till slut, med mer eller mindre hjälp, har lyckats föra in den avgörande hjälpkonstruktionen, triangeln som visas i fig. 1, bör läraren övertyga sig om att eleverna kan se tillräckligt långt framåt i lösningen innan han uppmanar dem att börja med själva räkningarna.
"Jag tror det var en bra idé att rita den här triangeln. Nu har vi en triangel, men var har vi det som söks?"
"Det som söks är hypotenusan i en triangel, och den kan vi beräkna med hjälp av Pytagoras sats."
"Ja det kan ni, om båda de andra sidorna är kända. Men är de det?"
"En av sidorna, c, är given. Och den andra kan väl inte vara svår att finna. Ja, visst ja! Den andra sidan är själv hypotenusa i en annan rät triangel."
"Mycket bra! Nu har ni planen klar."
11. Att genomföra planen. Att utarbeta en plan, att komma på idén till en lösning är inte lätt. Det krävs mycket för att lyckas: tidigare förvärvade kunskaper, sunda tankevanor, målmedveten koncentration och en sak till — en god portion tur. Att genomföra planen är mycket lättare. Vad vi då behöver är huvudsakligen tålamod.
Planen ger lösningen i stora drag. Vi måste övertyga oss om att detaljerna passar in i den, och därför måste vi tålmodigt undersöka den ena detaljen efter den andra, tills allting är fullkomligt klart. Ingen mörk vrå får återstå där något fel skulle kunna vara gömt.
Om eleven verkligen har kommit fram till en plan kan läraren ta det relativt lugnt ett tag. Den stora risken är nu att eleven glömmer planen. Detta händer lätt om han tar emot planen utifrån och accepterar den på grund av lärarens auktoritet. Om han däremot har utarbetat den själv, t.o.m. med en del hjälp, och är belåten med sin slutliga uppfattning, kommer han inte att glömma tankegången så lätt. Likväl måste läraren stå fast vid att eleven bör kontrollera varje steg.
Vi kan övertyga oss om att ett visst steg i vår argumentation är korrekt antingen "intuitivt" eller "formellt". Vi kan koncentrera oss på punkten i fråga tills den blir så klar och tydlig att det inte finns något tvivel om att steget är riktigt. Vi kan också komma fram till riktigheten genom att använda formella regler. (Skillnaden mellan "insikt" och "formellt bevis" är tillräckligt klar i många viktiga fall, så vi kan överlämna ytterligare diskussion åt filosofer.)
Huvudsaken är att eleven är uppriktigt övertygad om att varje steg är korrekt. I vissa fall kan det vara lämpligt. att läraren framhäver skillnaden mellan att "inse" och att "bevisa": Kan du klart se att steget är korrekt? Men kan du även bevisa att steget är riktigt?
12. Exempel. Låt oss sammanfatta vårt arbete fram till den punkt där vi lämnade det i slutet av avsnitt 10. Eleven har, till slut fått en föreställning om lösningen. Han har ett utkast till den. Han ser den räta triangel, i vilken den okända storheten x är hypotenusa och den givna höjden c är en av sidorna. Den andra sidan är diagonal i en yta. Eleven måste möjligen uppmanas att införa lämpliga beteckningar. Han borde välja y för att beteckna den andra sidan, diagonalen i den yta vars sidor är a och b. På det viset kan han klarare se lösningens idé, som ligger i att införa ett hjälpproblem där den okända storheten är y. Till slut erhåller han genom att betrakta den ena räta triangeln efter den andra (se fig. 1) x² = y² + c² och y² = a² + b² och därefter, genom att eliminera hjälpstorheten y, x² = a² + b² + c² och x = √(a² + b² + c²).
Läraren har ingen anledning att avbryta eleven om denne utför detaljerna korrekt utom möjligen för att varna honom
och påpeka att han måste kontrollera varje steg. Läraren kan t.ex. fråga:
"Kan du klart se att triangeln med sidorna x, y, c är en rät triangel?"
På denna fråga kanske eleven uppriktigt svarar jakande, men han skulle kunna bli helt förvirrad och hindrad om en lärare som inte är nöjd med elevens intuitiva övertygelse skulle fortsätta med frågan:
"Men kan du bevisa att triangeln är rät?"
Med andra ord bör läraren hellre undvika denna fråga, såvida inte klassen har fått en viss utbildning i rymdgeometri. Men även i ett sådant fall kan det finnas stor risk att svaret på denna i sammanhanget oväsentliga fråga kan komma att utgöra den största stötestenen för flertalet elever.
13. Att se tillbaka. Även ganska dugliga elever slår normalt ihop sina böcker och börjar titta efter någonting annat så snart de kommit fram till och skrivit ner lösningen på ett problem. När de gör det missar de en viktig och lärorik fas i arbetet. Genom att se tillbaka på den fullbordade lösningen, genom att ompröva och igen undersöka resultatet och den väg som ledde dit, skulle de kunna befästa sina kunskaper och utveckla sin förmåga att lösa problem. En god lärare bör själv förstå att det inte finns några problem som kan behandlas på ett fullständigt uttömmande sätt, och han bör även överföra denna tankegång på sina elever. Det finns alltid någonting kvar att göra. Vi kan alltid förfina och fördjupa, vi kan förbättra varje lösning, och vi kan i vilket fall som helst alltid förbättra vår egen förståelse av lösningen.
. Eleven har nu genomfört sin plan. Han har skrivit ner lösningen och kontrollerat varje steg. Då borde han ha goda skäl att tro att hans lösning är korrekt. Icke desto mindre är det lätt att göra fel, speciellt om resonemanget är långt och invecklat. Därför är det önskvärt att kunna bevisa resultatet. Särskilt som det kanske kan finnas någon snabb och intuitiv metod för att testa antingen resultatet eller resonemanget skall man aldrig bortse från en sådan möjlighet. Kan du kontrollera resultatet? Kan du kontrollera bevisföringen?
För att övertyga oss om närvaron av eller egenskaperna hos ett föremål vill vi gärna se och röra vid det. På samma sätt som vi föredrar att uppfatta något med hjälp av två olika sinnen, så föredrar vi också att övertyga oss med hjälp av två olika bevis. Kan du härleda resultatet på något annat sätt? Naturligtvis föredrar vi ett kort och intuitivt resonemang framför ett långt och tungt: Kan du se det direkt?
En av lärarens första och främsta plikter är att inte ge sina elever intrycket att matematiska problem har föga samband med varandra och att de inte har något samband alls med någonting annat. När vi ser tillbaka på ett problems lösning har vi ett naturligt tillfälle att undersöka problemets samband med andra förhållanden. Eleverna kommer att tycka att det är intressant att se tillbaka på lösningen om de har gjort en uppriktig ansträngning och om de är medvetna om att de har uträttat någonting. Då blir de också angelägna att se vad annat de skulle ha kunnat åstadkomma med denna ansträngning, och hur de skall kunna klara av saken lika bra en annan gång. Läraren bör uppmuntra eleverna att föreställa sig fall där den genomgångna proceduren skulle kunna användas eller där resultatet skulle kunna utnyttjas. Kan du använda resultatet eller metoden för något annat problem?
14. Exempel. I avsnitt 12 kom eleverna slutligen fram till en lösning. Om de tre kantlängderna i den rektangulära parallellepipeden är a, b och c är diagonalen √(a2 + b2 + c2).
Kan du kontrollera resultatet? Läraren kan inte vänta sig något bra svar på denna fråga från oerfarna elever. Eleverna bör emellertid på ett ganska tidigt stadium göra erfarenheten att problem "i bokstäver" har en stor fördel över rent numeriska: problem. Om problemet är givet "i bokstäver" kan dess resultat prövas på många olika sätt, vilket man inte alls kan göra med ett problem "i siffror". Fastän vårt exempel är mycket enkelt räcker det för att belysa detta. Läraren kan ställa åtskilliga frågor om resultatet, vilka eleverna lätt kan besvara med "ja", medan svaret "nej" skulle ange en allvarlig defekt hos resultatet.
"Använde du alla du givna uppgifterna? Finns alla de givna storheterna a, b och c med i din slutliga formel för diagonalen?"
"Längd, bredd och höjd spelar samma roll i vår fråga. Vårt problem är symmetriskt med avseende på a, b och c. Är det uttryck som vi kommit fram till för diagonalen också symmetriskt i a, b och c? Förblir det oförändrat om a, b och c byter plats?"
"Vårt problem tillhör rymdgeometrin: Att finna diagonalen i en parallellepiped med givna dimensioner a, b och c. Vårt problem är analogt med ett problem i den plana geometrin: Att finna diagonalen i en rektangel med givna dimensioner a, b. Är resultatet av vårt rumsproblem analogt med resultatet av vårt plana problem?"
"Om höjden c minskar för att slutligen bli noll, kommer parallellepipeden att övergå i en parallellogram. Om du sätter c = 0 i din formel, får du då den riktiga formeln för diagonalen i en rektangulär parallellogram?"
"Om höjden c ökar, ökar diagonalens längd. Visar formeln att det är så?"
"Om alla tre längderna a, b och c i parallellepipeden ökar i samma proportion, kommer diagonalen också att öka i samma proportion. Om du sätter in 12a, 12b, 12c i stället för resp a, b, c i din formel, borde hela uttrycket för diagonalen som följd därav bli multiplicerad med en faktor 12. Förhåller det sig så?"
"Om a, b och c mäts i cm ger formeln också diagonalens längd mätt i cm, men om du ändrar alla mått till m bör formeln fortfarande vara riktig. Är den det?"
(De två sista frågorna är i huvudsak ekvivalenta, se Dimensionstest.)
Dessa frågor har åtskilliga goda effekter. För det första kan en intelligent elev knappast undgå att imponeras av det faktum att formeln kan klara så många tester. Han var redan övertygad om att formeln är riktig eftersom -han har härlett den noggrant. Men nu är han än mer övertygad, och hans ökade tilltro kommer från ett helt annat håll. Den kommer från. ett slags "experimentellt bevis". Tack vare frågorna får vidare formelns detaljer ny innebörd, och de länkas ihop med olika fakta. Det är därför lättare att komma ihåg formeln. Elevens kunskaper befästs. Slutligen kan frågorna lätt överföras på liknande problem. Efter någon erfarenhet med liknande problem börjar en intelligent elev förstå de underliggande allmänna idéerna: användning av alla relevanta data, variation av dessa data, symmetri, analogi. Om han lägger sig till med vanan att koncentrera sin uppmärksamhet mot sådana punkter kommer hans förmåga att lösa problem definitivt att öka.
Kan du kontrollera bevisföringen? Att åter gå igenom bevisföringen steg för steg kan vara nödvändigt i svåra och viktiga fall. Vanligtvis räcker det med att plocka ut svaga punkter för kontroll. I vårt fall kan det vara tillrådligt att i efterhand diskutera den fråga som var mindre lämplig att diskutera så länge vi ännu inte hade kommit fram till lösningen: Kan du bevisa att triangeln med sidorna x, y och c är en rät triangel? (Se slutet av avsnitt 12.)
Kan du använda resultatet eller metoden för något annat problem? Med litet uppmuntran och efter ett eller två exempel finner eleverna själva lätt tillämpningar, som huvudsakligen består i att ge någon konkret tolkning av problemets abstrakta matematiska delar. Läraren använde en sådan konkret tolkning när han tog klassrummet som exempel på problemets parallellepiped. En trög elev skulle kanske kunna föreslå som tillämpning att beräkna diagonalen i matsalen i stället för diagonalen i klassrummet. Om eleverna inte frivilligt kommer med några fantasifullare kommentarer kan läraren själv . formulera ett något annorlunda problem, t.ex.: "Om längd, bredd och höjd är givna för en rektangulär parallellepiped, sök avståndet från centrum till ett av hörnen."
Eleverna kan nu använda resultatet till problemet de nyss löst, om de ser att det sökta avståndet är halva den diagonal som de just beräknat, eller också kan de använda metoden och införa lämpliga räta trianglar. (I det föreliggande fallet vore detta senare alternativ något långsökt och klumpigt.)
Efter denna tillämpning kan läraren diskutera konfigurationen av parallellepipedens fyra diagonaler, eller de sex pyramider som har de sex sidoytorna som baser, spetsen i centrum och halvdiagonalerna som kanter. När elevernas geometriska föreställningsförmåga har friskats upp tillräckligt bör läraren återkomma till sin fråga: Kan du använda resultatet eller metoden för något annat problem? Nu är möjligheten större att eleverna kommer på någon intressantare konkret tolkning, t.ex. följande:
"En 8 m hög flaggstång skall sättas upp på taket av en skyskrapa. Den skall stå i mitten av taket som är 21 m långt och 16 m brett och skall stagas med hjälp av 4 likadana kablar. Kablarna skall fästas 2 m under flaggstångens topp och gå till hörnen av byggnadens tak. Hur lång skall varje kabel vara?"
Eleverna kan använda metoden från problemet vi nyss löst i detalj genom att införa en rät triangel i ett vertikalplan och en annan i ett horisontalplan. Eller också kan de använda resultatet och föreställa sig en av de fyra kablarna som diagonalen, x, i en rektangulär parallellepiped vars kanter är a = 10,5, b = 8, c = 6. Genom att direkt tillämpa formeln ser vi att x = 14,5. För ytterligare exempel, se Kan du använda resultatet?
15. Olika angreppsmetoder. Låt oss ännu en stund uppehålla oss vid det problem vi betraktat i avsnitten 8, 10, 12 och 14. Det huvudsakliga arbetet, att finna en plan för lösningen, beskrevs i avsnitt 10. Låt oss konstatera att läraren skulle ha kunnat gå fram på ett annat sätt. Om han. utgick från samma punkt som i avsnitt 10, skulle han ha kunnat gå en något annorlunda väg genom att ställa följande frågor:
"Känner ni till något närbesläktat problem?"
"Känner ni till något analogt problem?"
"Ni ser att problemet handlar om rymdgeometri. Skulle ni kunna komma på ett enklare analogt problem i plan geometri?"
"Som ni ser handlar problemet om en geometrisk figur i rummet. Det handlar om diagonalen i en rektangulär parallellepiped. Vilket skulle vara ett analogt problem om en figur i planet? Det skulle handla om — diagonalen — i en — rektangulär — "
"Parallellogram."
Även om eleverna är mycket långsamma och likgiltiga och tidigare inte kunde gissa någonting, måste de nu slutligen bidra med åtminstone någon om än obetydlig del av idén. För övrigt borde läraren om eleverna är så tröga aldrig ta upp det föreliggande problemet om parallellepipeden utan att ha förberett eleverna genom att först diskutera det analoga problemet om parallellogrammen. I så fall kan han nu fortsätta på följande sätt:
"Här är ett närbesläktat problem som ni löst förut. Kan ni använda det?"
"Skulle ni kunna införa någon hjälpkonstruktion så att ni kan använda det?"
Slutligen kanske läraren lyckas antyda den önskade idén för eleverna. Den består i att föreställa sig diagonalen i den givna parallellepipeden som en diagonal i en lämplig parallellogram, vilken måste införas i figuren (som parallellepipedens skärning med ett plan som går genom två motsatta kanter). Idén är i huvudsak densamma som förut (avsnitt 10) men angreppspunkten är en annan. I avsnitt 10 etablerades kontakten med elevernas tillgängliga kunskaper genom den obekanta storheten. Ett tidigare löst problem togs upp därför att det hade samma obekanta storhet som det givna problemet. I det föreliggande avsnittet skapas kontakten genom analogi.
16. Lärarens frågemetod (visad i avsnitten 8, 10, 12, 14 och 15) är huvudsakligen denna: Börja med en allmän fråga eller uppmaning på listan. Gå sedan om nödvändigt successivt ner till mer specifika och konkreta frågor eller uppmaningar tills någon framkallar gensvar hos eleverna. Om man måste hjälpa en elev att utnyttja sin idé, börja då om möjligt igen med allmänna frågor eller uppmaningar på listan, och återvänd sedan till mer speciella om det behövs.
Vår lista är naturligtvis bara en första lista av detta slag. Den tycks vara tillräcklig för flertalet enkla fall, men det är ingen tvekan om att den skulle kunna förbättras. Det är emellertid viktigt att uppmaningarna och förslagen som vi börjar med är enkla, naturliga och generella, och att listan som upptar dem är kort.
Uppmaningarna måste vara enkla och naturliga eftersom de annars inte kan vara diskreta.
Uppmaningarna måste vara generella och tillämpbara inte bara på det aktuella problemet utan på problem av alla slag, om de skall kunna utveckla elevens förmåga och inte enbart en speciell teknik.
Listan måste vara kort för att frågorna skall kunna upprepas ofta, naturligt och under olika omständigheter. Därigenom finns möjligheten att eleven så småningom börjar använda dessa frågor, som då hjälper honom att utveckla en tankevana.
Det är nödvändigt att först småningom komma ner till specifika förslag och uppmaningar, för att eleven skall få en så stor del i arbetet som möjligt.
Den här metoden att fråga är inte stel. Lyckligtvis kan man säga, ty i sådana här sammanhang är varje stel, mekanisk och pedantisk procedur med nödvändighet dålig. Vår metod tilllåter en viss elasticitet och variation. Den tillåter olika sätt att angripa problemet (avsnitt 15), den kan och bör tillämpas så att frågor som läraren ställer skulle ha kunnat komma från eleven själv.
Om en läsare önskar använda den metod som föreslås här i sin egen undervisning, måste han naturligtvis gå fram med varsamhet. Han bör noggrant studera exemplet i avsnitt 8 och de följande exemplen i avsnitt 18, 19 och 20. Han bör omsorgsfullt förbereda de exempel han ämnar diskutera och även tänka ut olika angreppsmetoder. Han bör börja med några försök för att så småningom komma underfund med hur han kan handskas med metoden, hur eleverna reagerar och hur lång tid den tar.
17. Bra frågor och dåliga frågor. Har man förstått den frågemetod som formulerats ovan kan man ha nytta av den för att genom jämförelse bedöma värdet av och egenskaper hos vissa uppmaningar som kan riktas och ofta riktas i avsikt att hjälpa elever.
Låt oss gå tillbaka till situationen så som den framställdes i början av avsnitt 10 när följande fråga ställdes: Känner ni till något närbesläktat problem? I stället skulle man, i bästa avsikt att hjälpa eleverna, ha kunnat ställa frågan: Skulle ni kunna tillämpa Pytagoras sats?
Avsikten må vara den bästa, men frågan är nästan den sämsta man kan tänka sig. Om vi tänker på i vilket sammanhang den ställs kommer vi att finna en lång rad invändningar mot detta slag av "hjälp".
1. Om eleven är nära lösningen kanske han kan förstå den uppmaning som ligger i frågan, men om han inte är det, kommer han troligen inte alls att inse meningen med den. Därför ger inte frågan någon hjälp när hjälpen behövs som mest.
2. Om uppmaningen förstås avslöjar den hela hemligheten. Mycket litet återstår för eleven att göra.
3. Uppmaningen är för speciell till sin natur. Även om eleven kan använda sig av den för att lösa det aktuella problemet lär han ingenting för framtida problem. Frågan är inte lärorik.
4. Även om eleven förstår uppmaningen kan han knappast förstå hur läraren kunde komma på idén att ställa en sådan fråga. Och hur skulle han, eleven, själv kunna komma på en sådan fråga? Den kommer som en onaturlig överraskning, som en kanin framtrollad ur en hatt. Den är verkligen inte alls lärorik.
Ingen av dessa invändningar kan resas mot den procedur som beskrivs i avsnitt 10 eller mot den som beskrivs i avsnitt 15.
FLER EXEMPEL
18. Ett konstruktionsproblem. Inskriv en kvadrat i en given triangel. Två av kvadratens hörn skall ligga på triangelns bas, de andra två hörnen på triangelns övriga sidor, en på vardera sidan.
"En kvadrat."
"Vad är det som är givet?"
"En triangel är given, ingenting annat."
"Hur lyder villkoret?"
"Kvadratens fyra hörn skall ligga på triangelns omkrets, två hörn på basen, ett hörn på vardera av de andra två sidorna."
"Är det möjligt att uppfylla villkoret?"
"Jag tror det. Jag är inte säker."
"Du tycker tydligen inte att problemet är alltför lätt. Om du inte kan lösa det givna problemet, försök först lösa något liknande problem. Skulle du kunna uppfylla en del av villkoret?"
"Vad menas med en del av villkoret?"
| Fig. 2 | 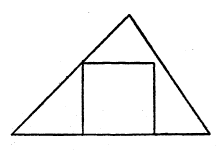 |
"Som du ser handlar villkoret om kvadratens alla hörn. Hur många hörn finns det?"
"Fyra."
"En del av villkoret skulle handla om mindre än fyra hörn. Behåll endast en del av villkoret, förkasta den andra delen. Vilken del av villkoret är lätt att uppfylla?"
"Det är lätt att rita en kvadrat med två hörn på triangelns omkrets — eller t.o.m. en med tre hörn på omkretsen!" "Rita en figur!"
Eleven ritar fig. 2.
"Du har behållit endast en del av villkoret och förkastat den andra delen. I vilken grad är den okända storheten nu bestämd?"
| Fig. 3 | 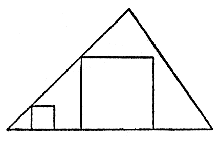 |
"Kvadraten är inte bestämd om den bara har tre hörn på triangelns omkrets."
"Bra! Rita en figur."
Eleven ritar fig. 3.
"Som du sade är kvadraten inte bestämd genom den del av villkoret du behållit. Hur kan den variera?"
"Tre av hörnen på din kvadrat ligger på triangelns omkrets men det fjärde hörnet ligger ännu inte där det skall ligga. Din kvadrat är, som du sade, inte bestämd. Den kan variera, detsamma gäller dess fjärde hörn. Hur kan det variera?"
"Gör ett experiment om du vill. Rita fler kvadrater med tre hörn på omkretsen på samma sätt som de två tidigare kvadraterna. Rita små kvadrater och stora kvadrater. Kan man säga någonting om orten för det fjärde hörnet? Hur kan det variera?"
Läraren har nu fört eleven mycket nära lösningens idé. Om eleven kan gissa att orten för det fjärde hörnet är en rät linje är saken klar. Då förstår han.
19. Ett, bevisproblem. Två vinklar ligger i skilda plan men vardera sidan i den ena är parallell med motsvarande sida i den andra och har också samma riktning. Bevisa att sådana vinklar är lika.
Vad vi skall bevisa är en fundamental sats i rymdgeometrin. Problemet kan ges till elever som kan plan geometri och känner till de få fakta om rymdgeometri som föregår och förbereder den aktuella satsen i Euklides Elementa. (Den sats vi har formulerat och vill bevisa är teorem 10 ur bok XI av Euklides.) Med kursiv stil skrivs nu inte bara frågorna och uppmaningarna från vår lista utan också andra, som motsvarar dessa på precis samma sätt som "bevisproblem" motsvarar "sökproblem". (Sammanhangen är systematiskt utarbetade i Sökproblem, bevisproblem 5, 6.)
| Fig. 4 | 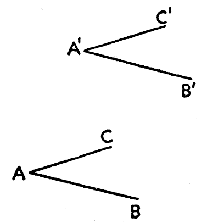 |
"Vad har vi för antagande?"
"Två vinklar ligger i skilda plan. Vardera sidan i den ena är parallell med motsvarande sida i den andra och har också samma riktning."
"Vad har vi för påstående?"
"Vinklarna är lika."
"Rita en figur. Inför lämpliga beteckningar."
Eleven drar linjerna i fig. 4 och väljer, mer eller mindre hjälpt av läraren, de bokstäver som visas där.
"Vad har vi för antagande? Försök att uttrycka det med våra beteckningar."
"A, B och C ligger inte i samma plan som A', B' och C'. AB||A'B', AC||A'C'. Dessutom är AB orienterad i samma riktning som A'B' och AC som A'C'."
"Vad har vi för påstående?"
"![]() BAC =
BAC = ![]() B'A'C'."
B'A'C'."
"Betrakta påståendet! Försök finna en känd sats som har samma eller liknande påstående."
"Om två trianglar är kongruenta är motsvarande vinklar lika stora."
"Utmärkt! Då har vi här en närbesläktad sats som är bevisad förut. Skulle du kunna använda den?"
"Ja, jag tror det, men jag vet inte riktigt hur."
"Skulle du kunna införa någon hjälpkonstruktion så alt du kan använda den?"
| Fig. 5 | 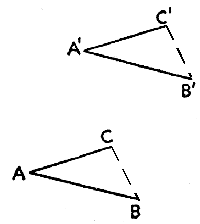 |
…
"Den sats som du citerade så bra handlade om trianglar, om ett par kongruenta trianglar. Har du några trianglar i figuren?"
"Nej. Men jag skulle kunna konstruera några. Jag kan förena B med C och B' med C'. Då får vi två trianglar, ΔABC och ΔA'B'C'."
"Inte illa. Men vad kan du använda dessa trianglar till?"
"Att bevisa påståendet ![]() BAC =
BAC = ![]() B'A'C'."
B'A'C'."
"Bra! Om du vill bevisa detta, vad behöver du då för slags trianglar?"
"Kongruenta trianglar. Javisst! Jag kan naturligtvis välja B, C och B', C' så att AB = A'B', AC = A'C'. "
"Förträffligt! Vad är det nu du skall bevisa?"
"Jag skall visa att trianglarna är kongruenta, att ΔABC ![]() ΔA'B'C'. Om jag kan bevisa det så följer påståendet
ΔA'B'C'. Om jag kan bevisa det så följer påståendet ![]() BAC =
BAC = ![]() B'A'C' omedelbart."
B'A'C' omedelbart."
"Just det! Du har fått ett nytt mål, du har kommit fram till ett nytt påstående. Betrakta påståendet! Försök finna en känd sats med samma eller liknande påstående."
"Två trianglar är kongruenta om — om de tre sidorna i den ena är lika med motsvarande tre sidor i den andra."
"Bravo! Du kunde ha valt en sämre sats. Nu har du igen en närbesläktad sats som är bevisad förut. Skulle du kunna använda den?"
"Jag skulle kunna använda den om jag visste att BC=B'C'."
"Alldeles riktigt! Vad måste du alltså göra?"
Visa att BC = B'C'.""Försök finna en känd sats med samma eller liknande påstående."
"Ja, jag vet en sats som slutar ’… så är de två linjerna lika’. Men den passar inte."
"Skulle du kunna införa någon hjälpkonstruktion så att du kan använda den?"
…
"Jo, hur skall du kunna visa att BC=B'C' när det inte finns något samband i figuren mellan BC och B'C'?"
…
"Använde du antagandet? Vad har vi för antagande?
"Vi antar att AB||A'B' och att AC||A'C'. Ja, det måste man naturligtvis använda sig av."
"Använde du hela antagandet? Du säger att AB||A'B'. Är det allt du vet om dessa linjer?"
"Nej. AB är också lika med A'B' genom konstruktion. De är parallella och lika stora. Och det gäller för AC och A'C' också."
"Två parallella linjer av samma längd — det är en intressant kombination. Har du sett den förut?"
"Ja visst, ja! En parallellogram! Jag kan förena A med A', B med B' och C med C'."
"Det är ingen dum idé. Hur många parallellogrammer har du nu i figuren?"
"Två. Nej, tre. Nej, två. Jag menar, det finns två som man direkt kan visa att de är parallellogrammer. Den tredje ser ut att vara det. Jag hoppas jag kan visa att den är det. Och i så fall kommer beviset att vara klart!"
Vi kunde ha rätt att anta av de tidigare svaren att eleven är intelligent. Men efter denna sista kommentar är det inget tvivel om att han är det.
Denna elev visar förmåga att gissa ett matematiskt resultat och han kan klart skilja mellan ett bevis och en gissning. Han vet också att gissningar kan vara mer eller mindre sannolika. Han har faktiskt lärt sig någonting av sin matematikundervisning. Han har verkligen erfarenhet av att lösa problem. Han kan komma på och utnyttja en god idé.
| Fig. 6 | 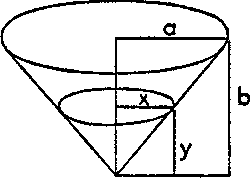 |
20. Ett hastighetsproblem. Vatten strömmar ut ur en kran och ner i en konisk behållare. Utströmningshastigheten (som vi t.ex. kan mäta i kubikmeter per minut) betecknar vi med u. Behållaren har formen av en rät cirkulär kon vars horisontella basyta har radien a. Konens spets pekar nedåt, höjden är b. Beräkna stigningshastigheten för vattenytan när vattendjupet är y. Beräkna slutligen hastigheten numeriskt genom att sätta in storheterna a = 4 m, b = 3 m, u = 2 m3/min och y = 1 m.
Eleverna antas känna till begreppet derivata samt de enklaste reglerna för derivering.
"Vad är det som är givet?"
"Basradien i konen är a = 4 m, konens höjd b = 3 m, hastigheten med vilken vattnet flyter in i behållaren u = 2 m3/min och vattendjupet i ett visst ögonblick y = 1 m."
"Riktigt. Problemets formulering verkar som en uppmaning att till en början bortse från de numeriska värdena för att i stället arbeta med bokstäver och uttrycka den obekanta med hjälp av a, b, u och y. Först på slutet sätter vi in de givna värdena för de olika storheterna. Jag skulle följa denna uppmaning. Nåväl, vad är det som söks?"
"Den hastighet med vilken ytan stiger när vattendjupet är y."
"Vad menar du med det? Skulle du kunna uttrycka det i andra ord?"
"Den hastighet med vilken vattendjupet ökar."
"Vad innebär det? Skulle du kunna formulera om det ytterligare?"
"Derivatan av vattendjupet med avseende på tiden."
"Det är riktigt, derivatan av y. Men vad är en derivata? Gå tillbaka till definitionen."
"Derivatan är ett mått på hur snabbt en funktion ändrar sig. Den är funktionens ändringshastighet."
"Ja. Men är y en funktion? Som vi sade förut bortser vi nu från det numeriska värdet av y. Kan du föreställa dig att y förändras?"
"Ja, vattendjupet y ökar med tiden."
"Då är alltså y en funktion av vad?"
"Av tiden t."
"Bra. Inför lämpliga beteckningar. Hur skulle du vilja skriva ändringshastigheten för y i matematiska symboler?
"dy/dt".
"Bra. Det är alltså detta som är den obekanta. Den måste alltså uttryckas med hjälp av a, b, u och y. För övrigt är en av dessa storheter en hastighet. Vilken?"
"u är den hastighet med vilken vatten strömmar in i behållaren."
"Vad innebär det? Skulle du kunna säga det med andra ord?"
"u är ändringshastigheten för vattenvolymen i behållaren, u är derivatan av vattenvolymen i behållaren."
"Vad innebär det? Skulle du kunna formulera om det ytterligare? Hur skulle du skriva det med lämpliga beteckningar?"
"u = dV/dt."
"Vad är V?"
"Vattenvolymen i behållaren vid tiden t."
"Bra. Alltså måste du uttrycka dy/dt med hjälp av a, b, dV/dt och y. Hur skall du göra det?"
…
"Om du inte kan lösa det givna problemet, försök först lösa något liknande problem. Om du inte kan se sambandet mellan dy/dt och de givna storheterna, så försök föra in något enklare samband som skulle kunna tjäna som språngbräda."
…
"Ser du inte att det finns andra samband? Är exempelvis y och V oberoende av varandra?"
"Nej. När y ökar måste V också öka."
"Alltså finns det ett samband mellan dem. Vad är det för samband?"
"Jo, V är volymen av konen med höjden y. Men konens radie vid basen är inte känd."
"Du kan väl undersöka den i alla fall. Kalla radien någonting, t.ex. x."
"Då är V = πx²y/3."
"Riktigt. Vad vet vi nu om x? Är den oberoende av y?" "Nej. När vattendjupet y ökar, ökar också radien av den fria ytan x."
"Då finns det alltså ett samband. Hur ser det ut?"
"Naturligtvis, likformiga trianglar, och jag har x : y = a : b."
"Det finns ett samband till. Jag skulle inte försumma att utnyttja det. Glöm inte att du ville veta sambandet mellan V och y.
"Jag har x = ay/b och får därav V =πa²y³/3b²."
"Utmärkt. Det här verkar vara en språngbräda, eller hur?
Men vi får inte glömma bort målet. Vad är det som söks?" "Ja, det är dy/dt."
"Du måste alltså finna ett samband mellan dy/dt, dV/dt och de andra storheterna. Och här har du ett samband mellan y, V och de andra storheterna. Vad bör vi då göra?"
"Derivera naturligtvis! Jag får dV/dt = (πa²y²/b²)(dy/dt). Där har vi det!"
"Fint! Och nu kan vi sätta in de numeriska värdena."
"Om a = 4, b = 3, dV/dt = u = 2, y = 1, så är 2 = (π·16·1/9)(dy/dt)."